Processing math: 100%

WAEC Mathematics Past Questions & Answers - Page 125

621.

The bar chart shows the marks distribution in am English test. What percentage of the students had marks ranging from 35 to 50?

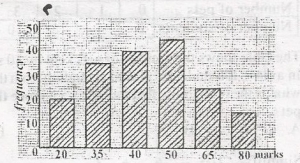
55 $\frac{1}{3}$ %

60%

65%

66 $\frac{2}{3}$ %

View answer & explanation

Correct answer is D

Percentage of students with marks ranging from 35 to 50 = $\frac{f_{35} + f{40} + f{50}}{\sum f}$

= $\frac{35 + 40 + 45}{20 + 35 + 40 + 45 + 25 + 15}$ x 100%

= $\frac{120}{180}$ x 100%

= 66 $\frac{2}{3}$ %

622.

The bar chart shows the marks distribution in am English test. If 50% is the pass mark, how many students passed the test?

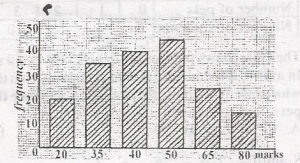
100

View answer & explanation

Correct answer is B

Pass mark = 50%

No. of students that passed = f₅₀ + f₆₅ + f₈₀

= 45 + 25 + 15

= 85

623.

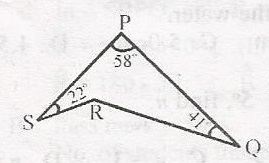
In the diagram, < PSR = 220^o, < SPQ = 58^o and < PQR = 41^o. Calculate the obtuse angle QRS.

90^o

100^o

121^o

60^o

View answer & explanation

Correct answer is C

Joining SQ. In $\bigtriangleup$ SPQ,

(22^o + a) + 55^o + (41^o + b) = 180^o

121^o + a + b = 180^o

a + b = 180 - 121

a + b = 59^o.....(1)

In $\bigtriangleup$ SRPQ; R + a + b = 180^o

R + 59^o = 180^o

(in (1), a + b = 59^o)

R = 180 - 59

R = 121^o

624.

In an athletic composition, the probability that an athlete wins a 100m race is $\frac{1}{8}$ and the probability that he wins in high jump is $\frac{1}{4}$ . What is the probability that he wins only one of the events?

$\frac{3}{32}$

$\frac{7}{3}$

$\frac{5}{3}$

$\frac{5}{16}$

View answer & explanation

Correct answer is D

Pr. (winning 100m race) = $\frac{1}{8}$

Pr. (losing 100m race) = 1 - $\frac{1}{8}$ = $\frac{7}{8}$

Pr. (winning high jump) = $\frac{1}{4}$

Pr. (losing high jump ) = 1 - $\frac{1}{4}$ = $\frac{3}{4}$

Pr. (winning only one) = Pr. (Winning 100m race and losing high jump) or Pr.(Losing 100m race and winning high jump)

= ( $\frac{1}{8} \times \frac{3}{4}$ ) + ( $\frac{7}{8} \times \frac{1}{4}$ )

= $\frac{3}{32} + \frac{7}{32}$

= $\frac{10}{32}$

= $\frac{5}{16}$

625.

The mean of the numbers 2, 5, 2x and 7 is less than or equal to 5. Find the range of the values of x

x $\leq$ 3

x $\geq$ 3

x < 3

x > 3

View answer & explanation

Correct answer is A

mean $\leq$ 5; $\frac{2 + 5 + 2x + 7}{4}$ $\leq$ 5

= $\frac{14 + 2x}{4} \leq 5$

= 14 + 2x $\leq$ 5 x 4

14 + 2x $\leq$ 20 ; 2x $\leq$ 20 - 14

2x $\leq$ 20 - 14

2x $\leq$ 6

x $\leq$ $\frac{6}{2}$

x $\leq$ 3