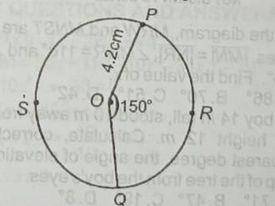
Find the area of the sector OPSQ
15.40cm\(^2\)
17.64cm\(^2\)
23.10cm\(^2\)
32.34cm\(^2\)
Correct answer is D
\(\frac{θ}{360}\) *π * r\(^2\) → \(\frac{210 * 22 * 4.2 * 4.2}{360 * 7}\)
\(\frac{1617}{50}\) = 32.34cm\(^2\)
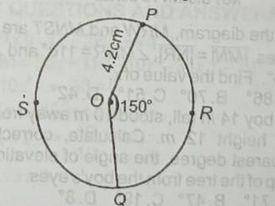
11cm
15.4cm
17.64cm
23.10cm
Correct answer is A
\(\frac{θ}{360}\) * 2 * π * r → \(\frac{150 * 2 * 22 * 4.2}{360 x 7}\)
= 11cm
An exterior angle of a regular polygon is 22.5°. Find the number of sides.
13
14
15
16
Correct answer is D
The sum of exterior angles of a polygon is 360°
\(\frac{360}{22.5}\) = 16 sides
Make t the subject of k = \(m \sqrt \frac{t-p}{r}\)
\(\frac{k^2r + p}{m^2}\)
\(\frac{k^2r + pm^2}{m^2}\)
\(\frac{k^2r - p}{m^2}\)
\(\frac{k^2r + p^2}{m^2}\)
Correct answer is B
square both sides to remove the square root
k\(^2\) = m\(^2\) \(\frac{t-p}{r}\)
\(\frac{k^2r}{m^2}\) = t - p
t = \(\frac{k^2r}{m^2}\) + p
t = \(\frac{k^2r + pm^2}{m^2}\)
Find the value of x such that \(\frac{1}{x}\) +\(\frac{4}{3x}\) - \(\frac{5}{6x}\) + 1 = 0
\(\frac{1}{6}\)
\(\frac{1}{4}\)
\(\frac{-3}{2}\)
\(\frac{-7}{6}\)
Correct answer is C
\(\frac{1}{x}\) +\(\frac{4}{3x}\) - \(\frac{5}{6x}\) + 1 = 0
using 6x as lcm
→ \(\frac{6+8-5+6x}{6x}\)
→ \(\frac{9+6x}{6x}\) = 0
9+6x = 0
6x = -9
x = \(\frac{-9}{6}\) or \(\frac{-3}{2}\)
WAEC Subjects
Aptitude Tests