If (x + 3) varies directly as y and x = 3 when y = 12, what is the value of x when y = 8?
1
\(\frac{1}{2}\)
\(-\frac{}{}\)
-1
Correct answer is A
\((x+3) \propto y\\
∴x + 3 = ky\hspace{1mm}when\hspace{1mm}x = 3, y = 12\\
3+3 = 12k\\
∴ k = \frac{1}{2}\\
\Longrightarrow x + 3 = \frac{1}{2}y\) to find x when y = 8
\(x + 3 = \frac{1}{2}\times 8\\
x=4-3\\
x = 1\)
2
3
7
9
Correct answer is B
20 members in the ratio 3:1
Number of women = \(\frac{1}{4} \times 20\)
= 5
Let the number of women to be added = x
Total number of members in the committee = 20 + x
\(\frac{5 + x}{20 + x} = \frac{2}{5}\)
\(5(5 + x) = 2(20 + x)\)
\(25 + 5x = 40 + 2x \implies 5x - 2x = 40 - 25\)
\(3x = 15 \implies x = 5\)
18km
13.4km
13km
10.4km
Correct answer is B
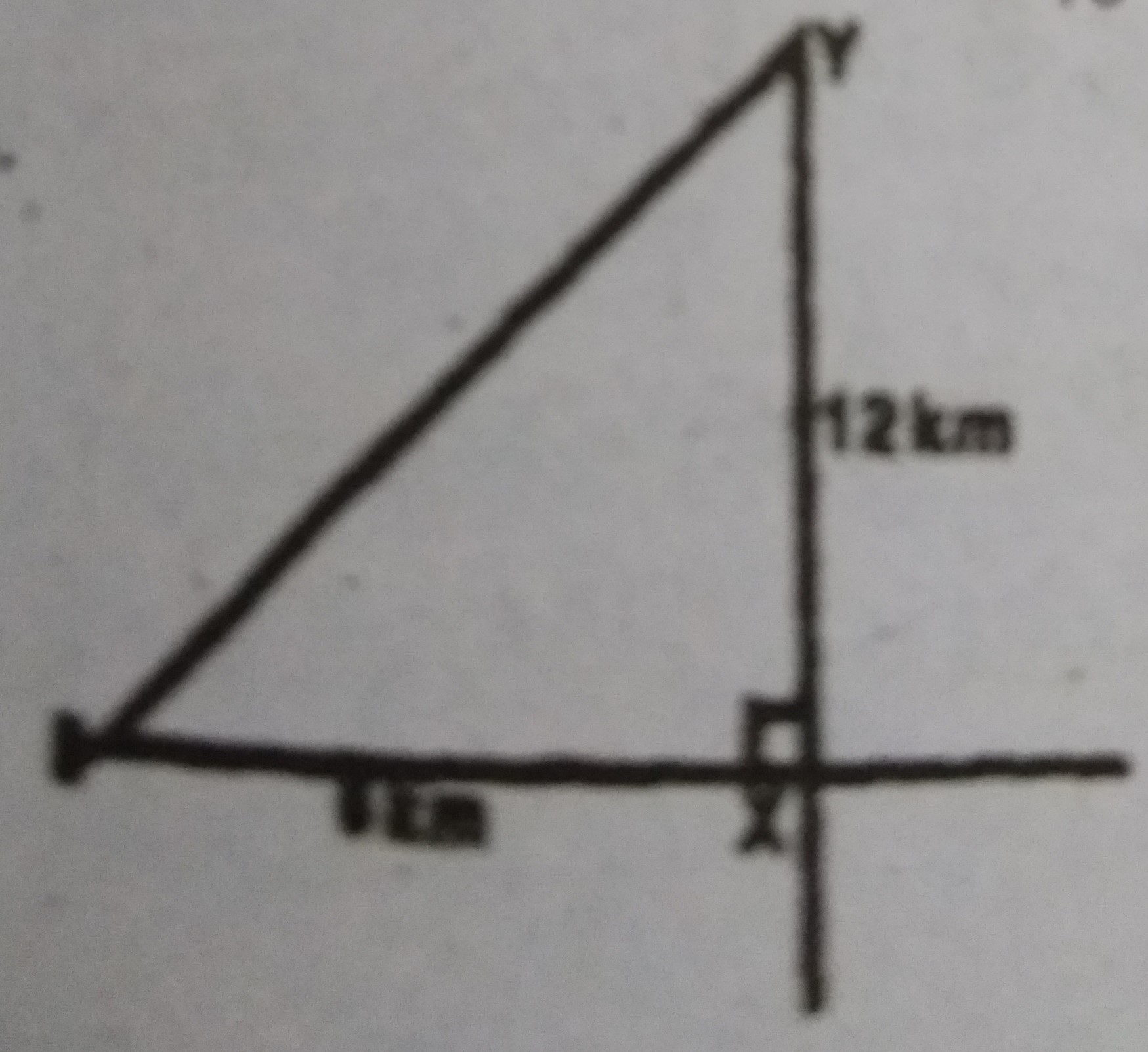
ZY\(^2\) = 12\(^2\) + 6\(^2\)
ZY\(^2\) = 144 + 36 = 180
ZY = \(\sqrt{180}\)
= \(13.416\)
= 13.4 km
6
5
4
-5
Correct answer is A
\(log2 = 0.3010\hspace{1mm}given\\
log2^y = 1.8062\\
∴ ylog2 = 1.8062\\
y=\frac{1.8062}{logy}=\frac{1.8062}{0.3010}=6\)
4
5
13
17
Correct answer is B
\((x + 2)^{2} = x^{2} + (x + 1)^{2}\)
\(x^2 + 4x + 4 = x^2 + x^2 + 2x + 1\)
\(2x^{2} - x^{2} + 2x - 4x + 1 - 4 = 0\)
\(x^{2} - 2x - 3 = 0\)
\(x^{2} - 3x + x - 3 = 0 \implies x(x - 3) + 1(x - 3) = 0\)
\((x - 3)(x + 1) = 0 \implies \text{x = 3 or -1}\)
\(x > 0 \implies x = 3\)
The longest side = 3 + 2 = 5.
WAEC Subjects
Aptitude Tests