Which of the following is not an exterior angle of a regular polygon?
66°
72°
24°
15°
Correct answer is A
No explanation has been provided for this answer.
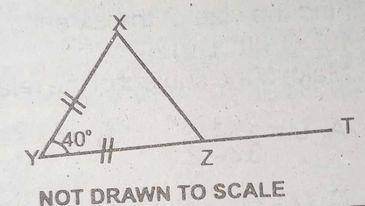
In the diagram, △XYZ is produced to T. if |XY| = |ZY| and ∠XYT = 40°, find ∠XZT
110°
130°
140°
180°
Correct answer is A
Isosceles Triangle. Two equal sides. Two equal angles ;
∠ X = ∠ Z
∠Y + ∠X + Z = 180 --> 40° + ∠X + ∠X = 180°
∠2X = 180° - 40° = 140°
∠X = 70°, i.e ∠X = 70 and ∠Z = 70°.
The exterior angle of triangle is the sum of two opposite internal angles
: ∠X + ∠Y = ∠XZT
=70° + 40° = 110°
The diagonal of a rhombus are 12cm and 5cm. calculate its perimeter
26cm
24cm
17cm
34cm
Correct answer is A
Perimeter of a Rhombus = 4L or 2√( d1\(^2\) + d2\(^2\))
P = 2√(12\(^2\) + 5\(^2\))
P = 2√(144 + 25)
P = 2√169 = 2 * 13
P = 26cm
If \(\frac{2}{x-3}\) - \(\frac{3}{x-2}\) = \(\frac{p}{(x-3)(x -2)}\), find p.
5 - x
- (x + 5)
13 - x
- (5x - 13)
Correct answer is A
\(\frac{2}{x-3}\) - \(\frac{3}{x-2}\)
= \(\frac{2(x -2) -3(x - 3)}{(x-3)(x -2)}\)
= \(\frac{2x -4 -3x + 9}{(x-3)(x -2)}\)
= \(\frac{5 - x}{(x-3)(x -2)}\)
if tanθ = \(frac{3}{4}\), 180° < θ < 270°, find the value of cosθ.
\(\frac{4}{5}\)
\(\frac{3}{5}\)
-\(\frac{4}{5}\)
-\(\frac{3}{5}\)
Correct answer is C
tanθ = \(frac{3}{4}\) → tanθ = 0.75
θ = tan\(^{-1}\)[0.75] → 36.8698°
cosθ = cos[36.8698°]
→ 0.800 or \(frac{4}{5}\)
However; in the third quadrant Cosine is negative
i.e -\(frac{4}{5}\)
WAEC Subjects
Aptitude Tests