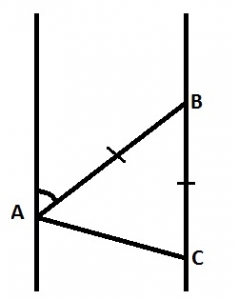
040o
070o
110o
290o
Correct answer is D
< ABC = 40° (alternate angles)
\(\therefore\) < ACB = \(\frac{180° - 40°}{2}\)
= 70°
\(\therefore\) Bearing of A from C = 360° - 70°
= 290°
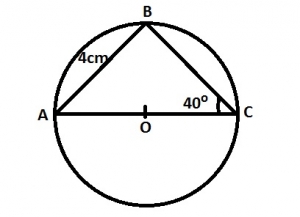
\(\frac{x}{sin 40^o}\)
\(\frac{x}{cos 40^o}\)
\(\frac{x}{2 sin 40^o}\)
\(\frac{x}{2 cos 40^o}\)
Correct answer is C
No explanation has been provided for this answer.
14.9 o
15.5 o
74.5 o
75.1 o
Correct answer is A
\(\tan x = \frac{20}{75} = 0.267\)
\(x = \tan^{-1} 0.267 = 14.93°\)
\(\approxeq\) 14.9°
If \(tan x = \frac{1}{\sqrt{3}}\), find cos x - sin x such that \(0^o \leq x \leq 90^o\)<
\(\frac{\sqrt{3}+1}{2}\)
\(\frac{2}{\sqrt{3}+1}\)
\(\frac{\sqrt{3}-1}{2}\)
\(\frac{2}{\sqrt{3}-1}\)
Correct answer is C
\(\cos x = \frac{\sqrt{3}}{2}\)
\(\sin x = \frac{1}{2}\)
\(\cos x - \sin x = \frac{\sqrt{3} - 1}{2}\)
If y varies inversely as x\(^2\), how does x vary with y?
x varies inversely as y2
x varies inversely as √y
x varies directly as y2
x varies directly as
Correct answer is B
\(y \propto \frac{1}{x^2}\)
\(y = \frac{k}{x^2}\)
\(x^2 = \frac{k}{y}\)
\(x = \frac{\sqrt{k}}{\sqrt{y}}\)
Since k is a constant, then \(\sqrt{k}\) is also a constant.
\(\therefore x \propto \frac{1}{\sqrt{y}}\)
WAEC Subjects
Aptitude Tests