if tanθ = \(frac{3}{4}\), 180° < θ < 270°, find the value of cosθ.
\(\frac{4}{5}\)
\(\frac{3}{5}\)
-\(\frac{4}{5}\)
-\(\frac{3}{5}\)
Correct answer is C
tanθ = \(frac{3}{4}\) → tanθ = 0.75
θ = tan\(^{-1}\)[0.75] → 36.8698°
cosθ = cos[36.8698°]
→ 0.800 or \(frac{4}{5}\)
However; in the third quadrant Cosine is negative
i.e -\(frac{4}{5}\)
Find The quadratic Equation Whose Roots Are -2q And 5q.
3x\(^2\) + 3qx - 10q\(^2\)
x\(^2\) + 3qx + 10q\(^2\)
x\(^2\) - 3qx + 10q\(^2\)
x\(^2\) - 3qx - 10q\(^2\)
Correct answer is D
x\(^2\) - (sum of roots)x + (products of roots) = 0
x\(^2\) - (-2q + 5q) + (-2q * 5q) = 0
x\(^2\) -(3q) + (-10q\(^2\)) = 0
x\(^2\) -3q - 10q\(^2\) = 0
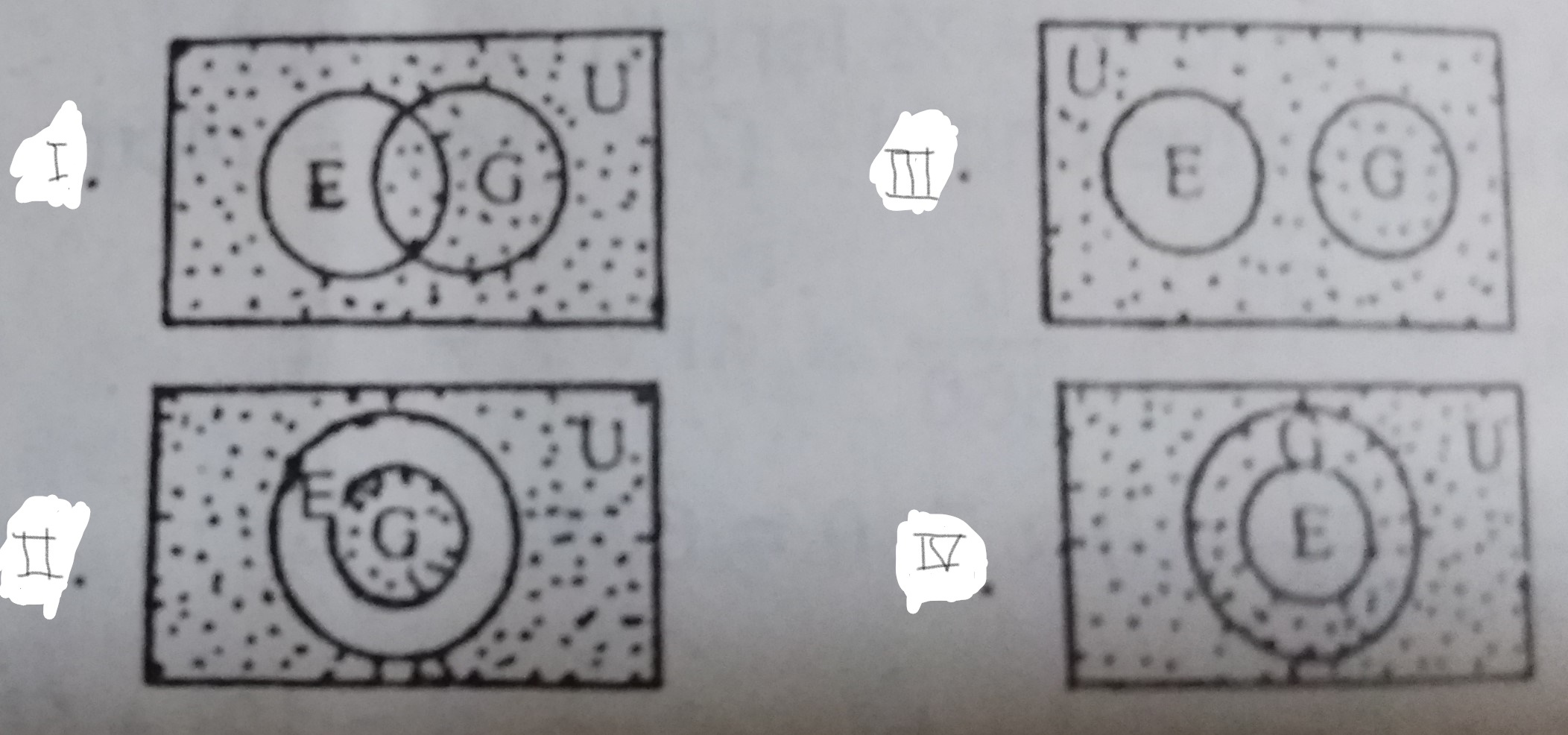
A
B
C
D
Correct answer is C
No explanation has been provided for this answer.
In △LMN, |LM| = 6cm, ∠LNM = x and sin x = sin x = \(\frac{3}{5}\). Find the area of △LMN
60cm\(^2\)
48cm\(^2\)
24cm\(^2\)
30cm\(^2\)
Correct answer is C
No explanation has been provided for this answer.
The height of an equilateral triangle of side is 10 3√ cm. calculate its perimeter.
20cm
60cm
40cm
30cm
Correct answer is B
Height of an equilateral triangle, h = a\(\frac{√3}{2}\), where a is the side of the equilateral triangle.
10√3 = a\(\frac{√3}{2}\)
cross multiply--> 2 * 10√3 = a√3
√3 strikes √3 on both sides
20 = a
The perimeter of an equilateral triangle is: P = 3a
P = 3 * 20 = 60cm
P = 30√3
WAEC Subjects
Aptitude Tests