Which of the following is not a sufficient condition for two triangles to be congruent?
AAS
SSS
SAS
SSA
Correct answer is D
No explanation has been provided for this answer.
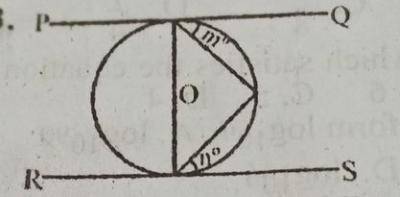
120\(^o\)
90\(^o\)
75\(^o\)
60\(^o\)
Correct answer is B
m + n + 90\(^o\) + 180\(^o\) (sum of angle in a \(\triangle\))
m + n = 180\(^o\) - 90\(^o\)
m + n =90\(^o\)
| x | 6.20 | 6.85 | 7.50 |
| y | 3.90 | 5.20 | 6.50 |
The points on a linear graph are as shown in the table. Find the gradient (slope) of the line.
2\(\frac{1}{2}\)
2
1
\(\frac{1}{2}\)
Correct answer is B
Gradient = \(\frac{y_2 - y_ 1}{x_2 - x_1}\)
= \(\frac{5.20 - 3.90}{6.85 - 6.20}\)
= \(\frac{1.3}{0.5}\)
= 2
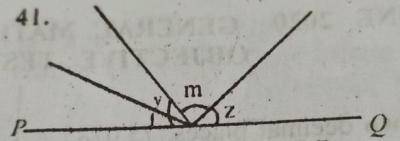
In the diagram, PQ is a straight line. If m = \(\frac{1}{2}\) (x + y + z), find value of m.
45\(^o\)
60\(^o\)
90\(^o\)
100\(^o\)
Correct answer is B
x + y + m + 2 = 180\(^o\)
\(\frac{x + y + 2}{2} + \frac{m}{2}\) = 90\(^o\)
m + \(\frac{m}{2} = 90^o\)
3m = 2 x 90\(^o\)
\(\frac{3m}{3} = \frac{180^o}{3}\)
m = 60\(^o\)
\(\frac{25}{144}\)
\(\frac{5}{33}\)
\(\frac{5}{6}\)
\(\frac{103}{132}\)
Correct answer is A
Pr(RR) = \(\frac{5}{12}\) = \(\frac{5}{12} \times \frac{5}{12} = \frac{25}{144}\)
WAEC Subjects
Aptitude Tests