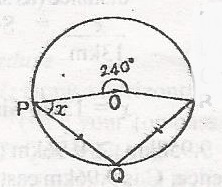
WAEC Past Questions and Answers - Page 2928

14,636.

In the diagram, PO and OR are radii, |PQ| = |QR| and reflex < PQR is 240^o. Calculate the value x

60^o

55^o

50^o

45^o

View answer & explanation

Correct answer is A

< Q = \(\frac{240}{2}\) (angle at centre twice that at the circumference)

< Q = 120^o

Also < POR = 360 - 240

= 120^o

( < s at centre) since /PQ/ = /QR/, < x = < R

Byt < x + < R + O + Q = 360 (sum of interior < s of quadrilateral)

x + R + 120 = 360^o

x + R = 360 - 240 = 120; Since x = R

x + x = 120

2x = 120

Since x = R

x + x = 120

2x = 120

x = \(\frac{120}{2}\)

= 60^o

14,637.

The diagram shows a cyclic quadrilateral PQRS with its diagonals intersecting at K. Which of the following triangles is similar to triangle QKR?

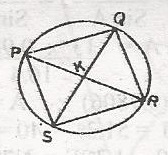
\(\bigtriangleup\) PQK

\(\bigtriangleup\) PKS

\(\bigtriangleup\) SKR

\(\bigtriangleup\) PSR

View answer & explanation

Correct answer is C

No explanation has been provided for this answer.

14,638.

A boy looks through a window of a building and sees a mango fruit on the ground 50m away from the foot of the building. If the window is 9m from the ground, calculate, correct to the nearest degree, the angle of depression of the mango from the window

9^o

10^o

11^o

12^o

View answer & explanation

Correct answer is B

tan \(\theta\) = \(\frac{9}{50}\) = 0.18

\(\theta = tan^{-1} 0.18\)

\(\theta\) = 10.20

14,639.

If 27^x = 9^y. Find the value of \(\frac{x}{y}\)

\(\frac{1}{3}\)

\(\frac{2}{3}\)

1\(\frac{1}{2}\)

View answer & explanation

Correct answer is B

27^x = 9^y

3^3x = 3^2y

3x = 2y

14,640.

In a quiz competition, a student answers n questions correctly and was given D(n + 50) for each question correctly answered. If he gets D600.00 altogether, how many questions did he answer correctly?

View answer & explanation

Correct answer is D

let the number of question = n

n(n + 50) = 600

n² + 50n - 600 - 0 by quadratic formular

x = \(\frac{b \pm \sqrt{b^2 - 4ac}}{2}\)

n = \(\frac{-50 \pm \sqrt{50^2 - 4(1) (-600)}}{2(1)}\)

= \(\frac{-50 \pm \sqrt{4900}}{2}\)

= \(\frac{-50 + 70}{2}\)

= \(\frac{20}{2}\)

= 10