0.0009Ω/π
100Ω
1030Ω
400Ω
2500Ω
Correct answer is D
Given Data: Frequency (F) = \(\frac{500}{π}\) , Inductance (L) = 0.9H, Capacitance (C) = \(2 \times 10^{-6}\)
Total circuit reactance = Inductive reactance ( X\(_L\) ) - Capacitive reactance ( X\(_C\) )
when ( X\(_L\) ) > ( X\(_C\) )
Inductive reactance ( X\(_L\) ) = 2πFL = 2 \(\times\) π \(\times\) \(\frac{500}{π}\) \(\times\) 0.9 = 900Ω
Capacitive reactance ( X\(_C\) ) = \(\frac{1}{2πFC}\) = \(\frac{1}{2 \times π \times 500/π \times 2 \times 10^{-6}}\)
= \(\frac{1}{2 \times 10^{-3}}\) = \(\frac{1}{0.002}\)
= 500Ω
Total circuit reactance = ( X\(_L\) ) - ( X\(_C\) ) = (900 - 500)Ω
=400Ω
8.00 x 106NC-1
4.00 x 106NC-1
4.00 x 10-4NC-1
2.00 x 10-4NC-1
2.50 x 10-1NC-1
Correct answer is B
F = qE; E = F/q = 40/(1.0 x 10-5) = 4.0 x 106
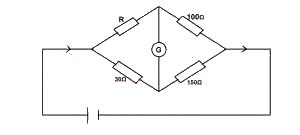
What is the value of R when G shows no deflection in the circuit illustrated above?
80Ω
75Ω
45Ω
20Ω
10Ω
Correct answer is D
R/30 = 100/150R = 20Ω
1.7 x 10-4V
3.4x10-4V
1.5x10-1V
6.0 x103V
1.2 x104V
Correct answer is D
No explanation has been provided for this answer.
4πεoq2r
qr/4πεo
q/4πεor
q2/4πεor
q2/4πεo
Correct answer is C
No explanation has been provided for this answer.
WAEC Subjects
Aptitude Tests