5.2cm
10.5cm
13.2cm
20.6cm
31.4cm
Correct answer is B
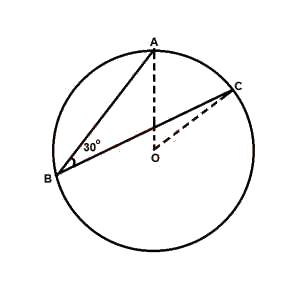
In the figure, < AOC = 2 x < ABC = 60° (angle subtended at the centre)
\(\therefore\) Arc AC = \(\frac{60}{360} \times 2 \times 10 \times 3.14\)
= \(\frac{31.4}{3}\)
= 10.466 cm \(\approxeq\) 10.5 cm
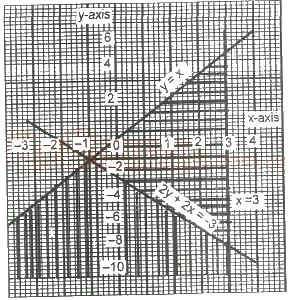
The area shaded with horizontal lines is the solution set of the inequalities;
y ≥ x, y + 3 ≥ 2x, x ≤ 3
y ≤ x, y + 2x ≥ -3, x ≤ 3
y ≤ -x, y + 2x ≤ 3, x ≥ -3
y ≥ -x, y + 3 ≤ 2x, x ≥ -3
y ≤ x, y ≤ 2x - 3, x ≥ 3
Correct answer is B
No explanation has been provided for this answer.
15
30
35
45
50
Correct answer is C
∩(E∩G) = ∩(E) + ∩(G) - ∩(E∩G) 80 = 65 + 50 - ∩(F∩G) ∴∩(E∩G) = 115 - 80 = 35
Let J be the set of positive integers, If H = {x: x∈J, x\(^2\) < 3 and x ≠ 0}, then
H = {1}
H is an infinite set
H = {0, 1, 2}
H = {}
J ≤ H
Correct answer is A
H = {x: x is a positive integer, x\(^2\) < 3 and x \(\neq\) 0}
H = {1}
Find the sum of the first five terms of the G.P 2,6, 18 ....
484
243
242
130
121
Correct answer is C
\(S_{n} = \frac{a(r^n - 1)}{r - 1}\)
a = 2; r = 6/2 = 3.
\(S_{5} = \frac{2(3^5 - 1)}{3 - 1}\)
= \(243 - 1 = 242\)
WAEC Subjects
Aptitude Tests