If tan y is positive and sin y is negative, in which quadrant would y lie?
First and third only
First and second only
Third only
Second only
Correct answer is C
No explanation has been provided for this answer.
₦(xy + 10)
₦(x + 10y)
₦(10x + y)
₦10(x + y)
Correct answer is D
Selling Price for each = ₦x + ₦y
= 10(₦x + ₦y)
76.11\(^o\)
53.67\(^o\)
52.40\(^o\)
51.32\(^o\)
Correct answer is B
Tan \(\theta\) = \(\frac{13.6}{10}\)
= tan\(^{-1}\)(1.36)
\(\theta\) = 53.67\(^o\)
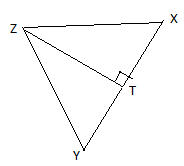
\(\frac{1}{\sqrt{3}}\)
\(\frac{\sqrt{3}}{2}\)
\(\sqrt{3}\)
\(\frac{1}{2}\)
Correct answer is A
ZT = \(\sqrt{6^2 - 3^2}\)
ZT = \(\sqrt{27}\) = \(3\sqrt{3}\)
tan (< XZT) = \(\frac{3}{3\sqrt{3}}\)
= - \(\frac{1}{\sqrt{3}}\)
Simplify; \(\frac{a}{b} - \frac{b}{a} - \frac{c}{b}\)
\(\frac{a - b + c}{ab}\)
\(\frac{ab - bc - ac}{ab}\)
\(\frac{a^2 - b^2 + ac}{ab}\)
\(\frac{a^2 - b^2 - ac}{ab}\)
Correct answer is D
\(\frac{a}{b} - \frac{b}{a} - \frac{c}{b}\)
\(\frac{a^2 - b^2- ac}{ab}\)
WAEC Subjects
Aptitude Tests