For what values of x is the expression \(\frac{3x-2}{4x^2+9x-9}\) undefined?
\(\frac{-3}{4} \hspace{1mm}or \hspace{1mm}3\)
\(\frac{-2}{3} \hspace{1mm}or \hspace{1mm}-3\)
\(\frac{2}{3} \hspace{1mm}or \hspace{1mm}3\)
\(\frac{3}{4} \hspace{1mm}or \hspace{1mm}-3\)
Correct answer is D
The equation \(\frac{3x - 2}{4x^2 + 9x - 9}\) is undefined when the denominator = 0.
\(4x^2 + 9x - 9 = 0\)
\(4x^2 + 12x - 3x - 9 = 0\)
\(4x(x + 3) - 3(x + 3) = 0\)
\((4x - 3)(x + 3) = 0\)
x = \(\frac{3}{4}\) or x = -3.
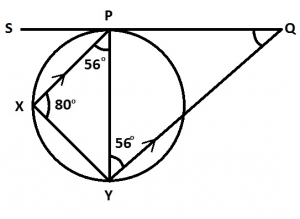
In the diagram, SQ is a tangent to the circle at P, XP||YQ, ∠XPY = 56o and ∠PXY = 80o.Find angle PQY
34o
13.36o
44o
46o
Correct answer is A
< XYQ = 180° - (80° + 56°)
= 44°
< PYQ = 56° (alternate angles, XP||YQ)
< QPY = 90°
< PQY = 180° - (90° + 56°)
= 34°
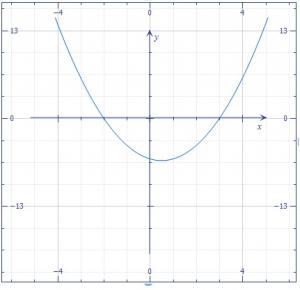
Which of the following is represented by the above sketch?
y = x2 + x - 6
y = x2 - x - 6
y = x2 - x + 6
y = x2 + x + 6
Correct answer is B
From the graph, the zeros of the equation exist at x = -2 and x = 3
\(\therefore\) (x + 2) = 0 and (x - 3) = 0
\(\implies (x + 2)(x - 3) = 0\)
\(x^2 - 3x + 2x - 6 = 0\)
\(x^2 - x - 6 = 0\) is the equation represented on the graph.
If (-3, -4) is a point on the line y = mx + 2 find the value of m.
-2
\(\frac{7}{4}\)
2
\(\frac{8}{3}\)
Correct answer is C
If (-3, -4) is a point on the line then
-4 = -3m + 2
-4 - 2 = -3m
-6 = -3m
m = 2
Find the nth term of the sequence 4, 10, 16 ,...
2(3n- 1)
2(2 + 3 n-1)
2 n + 2
2(3n+2)
Correct answer is A
\(T_{1} = 4; T_2 = 10; T_3 = 16\)
\(T_{2} - T_1 = T_3 - T_1 = 6\)
\(T_n = a + (n - 1) d\)
= \(4 + (n - 1) \times 6\)
= \(4 + 6n - 6\)
= \(6n - 2\)
= 2(3n - 1)
WAEC Subjects
Aptitude Tests