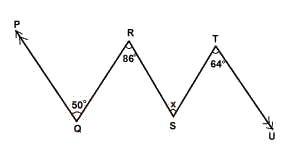
136o
120o
108o
100o
96o
Correct answer is D
No explanation has been provided for this answer.
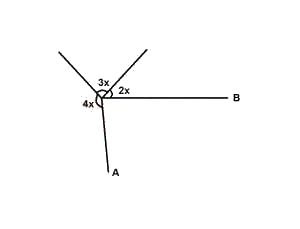
In the diagram above, AO is perpendicular to OB. Find x
7.5o
15o
22.5o
30o
38.6o
Correct answer is D
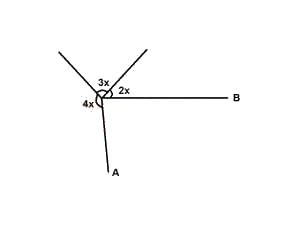
4x + 3x + 2x + 90 =360° [angle at a point]
9x + 90 = 360°
9x = 360° - 90°
9x = 270
x = 270/9
x = 30°
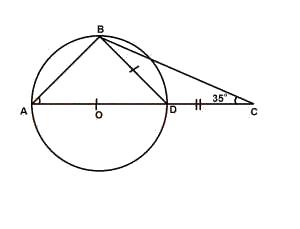
In the diagram above; O is the centre of the circle and |BD| = |DC|. If ∠DCB = 35°, find ∠BAO.
20o
25o
30o
35o
40o
Correct answer is A
< DBC = 35° (base angles of an isosceles triangle)
< CDB = 180° - (35° + 35°)
= 110°
< ADB = 70°; < ADB = 90°
\(\therefore\) < BAO = 180° - (70° + 90°)
= 20°
6 3/5cm
6 4/5cm
7 1/10cm
10 2/5cm
13 3/5cm,
Correct answer is E
Perimeter of sector = \(\frac{\theta}{360°} \times 2\pi r + 2r\)
= \(\frac{108}{360} \times 2 \times \frac{22}{7} \times \frac{7}{2} + 2(\frac{7}{2})\)
= \(6 \frac{3}{5} + 7\)
= \(13 \frac{3}{5} cm\)
31/2cm
7cm
1O1/2cm
14cm
21cm
Correct answer is B
The length of the arc subtended by the sector of angle 120° = circumference of the base of the cone.
\(\frac{120}{360} \times 2 \times \frac{22}{7} \times 21 = 2\pi r\)
\(44 = 2\pi r\)
\(r = 22 \div \pi\)
\(r = 22 \times \frac{7}{22}\)
r = 7 cm
WAEC Subjects
Aptitude Tests