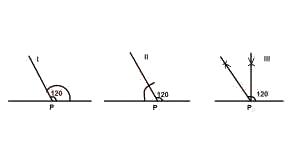
Which of the sketches above gives a correct method for constructing an angle of 120o at the point P?
I only
II only
III only
I and II only
I, II and III
Correct answer is D
No explanation has been provided for this answer.
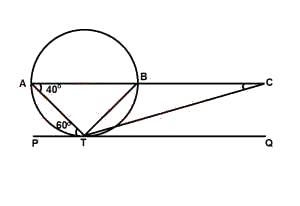
20o
30o
35o
40o
50o
Correct answer is E
From the figure < TAB = < BTQ = 40° (alternate segment)
\(\therefore\)< ATB = 180° - (70° + 40°) = 70° (angle on a straight line)
< BTC = \(\frac{40°}{2} = \frac{< BTQ}{2}\)
\(\therefore < BTQ = 40°\)
x° = 180° - (40° + 70° + 20°)
= 50°
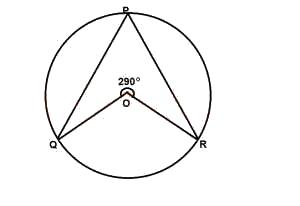
In the diagram below, O is the center of the circle if ∠QOR = 290o, find the size ∠QPR
110o
70o
55o
35o
20o
Correct answer is D
360o - 290o = 70o
70/2 = 35o

In the diagram above, PQRS is a cyclic quadrilateral, ∠PSR = 86o and ∠QPR = 38o. Calculate PRQ
58o
53o
48o
43o
38o
Correct answer is C
PQR = 180o - 86o = 94o
∴PRQ = 180o - 94o - 36o = 48o
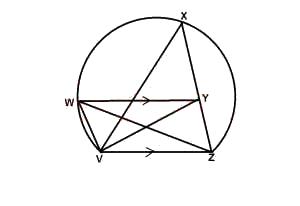
Which triangle is equal in area to ΔVWZ
ΔVXZ
ΔVYZ
ΔXYV
ΔWYV
ΔWYZ
Correct answer is B
Area of \(\Delta\) VYZ = Area of \(\Delta\) VWZ (same base and within same parallel)
WAEC Subjects
Aptitude Tests