21,171.
A.
11.25cm2
B.
12.83cm2
C.
22.0cm2
D.
67.2cm2
E.
90.2cm2
Correct answer is E

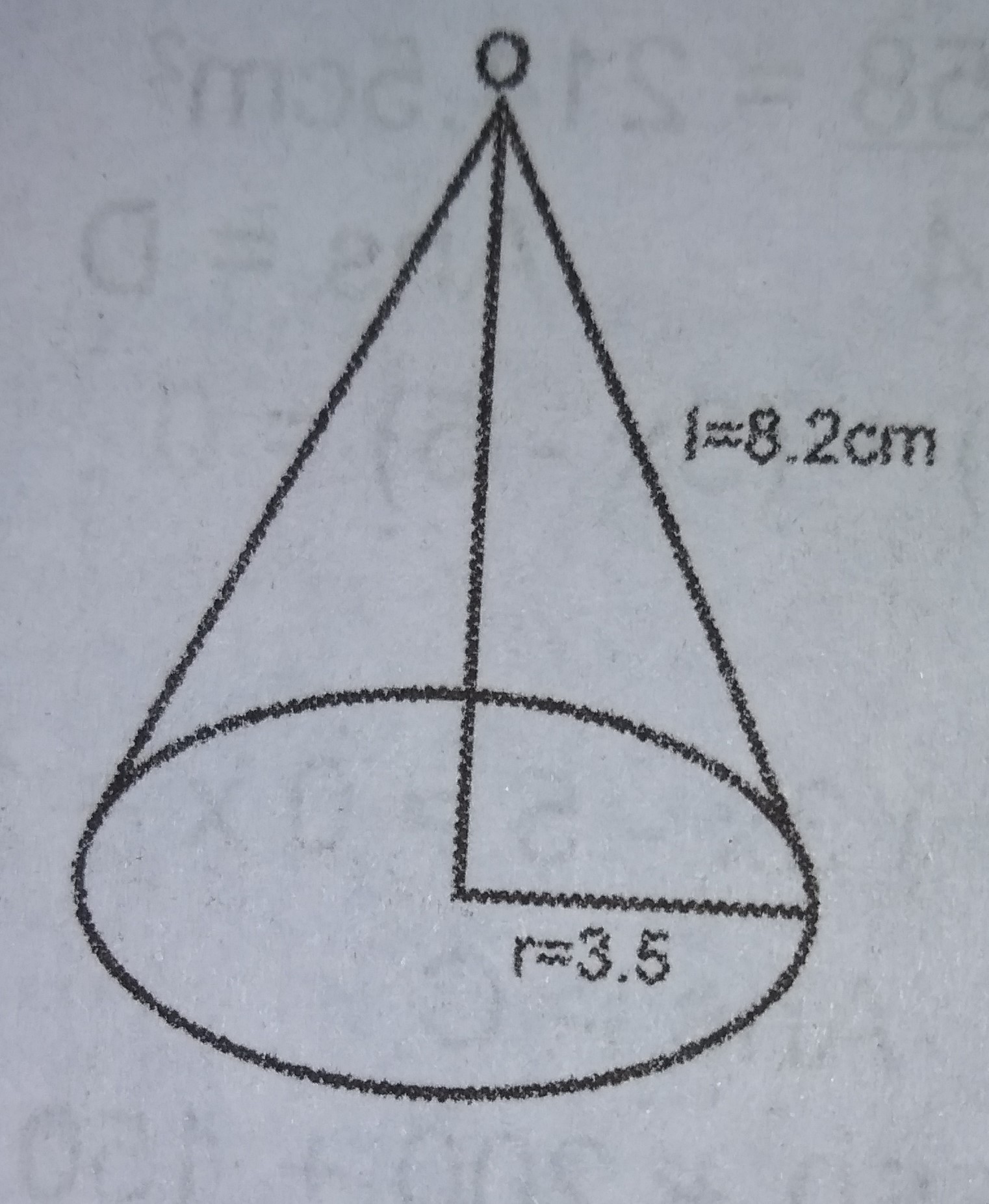
r = 3.5 cm; l = 8.2 cm.
Curved surface area = \(\pi rl\)
= \(\frac{22}{7} \times \frac{7}{2} \times \frac{41}{5}\)
= 90.2 cm\(^2\)
21,172.

A.
(0,6), (3,9)
B.
(-3, 0)(2,4)
C.
(-2,4)(3,9)
D.
(-2,3)(-3,2)
E.
(-2,2)(3,6)
Correct answer is C
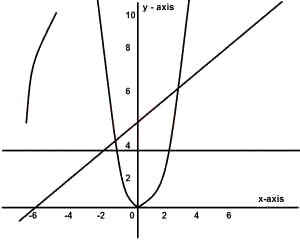
From the graph; when x = -2, y = 4
(-2, 4)
x = 3.0, y = 9; (3,9)
(-2, 4)(3,9)
21,173.

A.
55o
B.
40o
C.
35o
D.
25o
E.
20o
Correct answer is E
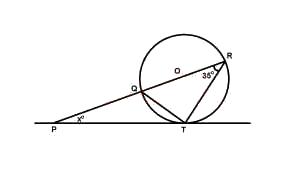
∠QPT = xo = 180o - 125o - 35o = 20o
21,174.
A.
\(9\frac{3}{7}cm^2\)
B.
\(12\frac{4}{7}cm^2\)
C.
\(18\frac{6}{7}cm^2\)
D.
\(25\frac{1}{7}cm^2\)
Correct answer is C
Area of a sector
\(\frac{θ}{360°} * πr^2\)
= \(\frac{135}{360} * 3.142 * 4 * 4\)
= \(18\frac{6}{7}cm^2\)
21,175.

A.
3/20
B.
1/5
C.
1/4
D.
3/10
E.
3/4
Correct answer is C
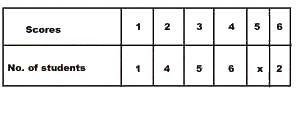
Probability = 5/20 = 1/4
WAEC Subjects
Aptitude Tests