27m
13.5 \(\sqrt{3m}\)
13.5 \(\sqrt{2m}\)
9\(\sqrt{3m}\)
Correct answer is D
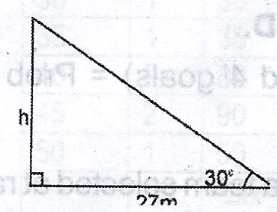
From the diagram,
tan 30\(^o\) = \(\frac{h}{27}\)
h = 27 tan 30\(^o\)
= 27 x \(\frac{1}{\sqrt{3}}\)
= \(\frac{27}{\sqrt{3}}\) x \(\frac{\sqrt{3}}{\sqrt{3}}\)
= \(\frac{27 \sqrt{3}}{3}\)
= 9\(\sqrt{3m}\)
Expression 0.612 in the form \(\frac{x}{y}\), where x and y are integers and y \(\neq\) 0
\(\frac{153}{250}\)
\(\frac{68}{111}\)
\(\frac{61}{100}\)
\(\frac{21}{33}\)
Correct answer is A
0.612 = \(\frac{0.612}{1}\) x \(\frac{1000}{1000}\)
= \(\frac{612}{1000}\)
= \(\frac{153}{250}\)
If x : y = \(\frac{1}{4} : \frac{3}{8}\) and y : z = \(\frac{1}{3} : \frac{4}{9}\), find x : z
2:3
3:4
3:8
1:2
Correct answer is D
\(\frac{x}{y}\) = \(\frac{1}{4} \div \frac{3}{8}\) = \(\frac{1}{4} \times \frac{8}{3}\) = \(\frac{2}{3}\)
\(\frac{y}{z}\) = \(\frac{1}{3} \div \frac{4}{9}\) = \(\frac{1}{3} \times \frac{9}{4}\) = \(\frac{3}{4}\)
But,
x = \(\frac{2}{5}T_1\), y = \(\frac{3}{5}T_1\)
y = \(\frac{3}{7}T_2\), z = \(\frac{4}{7}T_2\)
Using y = y
\(\frac{3}{5}T_1\) = x = \(\frac{3}{7}T_2\)
\(\frac{T_1}{T_2}\) = \(\frac{3}{7}\) x \(\frac{5}{3}\) = \(\frac{15}{21}\)
\(T_1 = 15\) and \(T_2 = 21\)
Thus , x = \(\frac{2}{5}\) x 15 = 6
y = \(\frac{3}{5}\) x 15 = 9
y = \(\frac{3}{7}\) x 21 = 9
z = \(\frac{4}{7}\) x 21 = 12
Hence; x : z = 6 : 12
= 1 : 2
Find the inter-quartile range of 1, 3, 4, 5, 8, 9, 10, 11, 12, 14, 16
6
7
8
9
Correct answer is C
\(Q_1 = \frac{1}{4}\) (N + 1)th
\(\frac{1}{4} \times 12^{th}\) no.
= 3rd no (\(\cong\) 4)
\(Q_3 = \frac{3}{4}\) (N + 1)th
= \(\frac{3}{4}\) x 12th no.
= 9th no. (\(\cong\) 12)
Hence, interquartile range
= \(Q_3 - Q_1\)
= 12 - 4
= 8
If 3x\(^o\) 4(mod 5), find the least value of x
1
2
3
4
Correct answer is C
3x \(\equiv\) 4(mod 5)
In modulo 5, multiples of 5 that give solution to the given equation are 5, 20, 35, 50,... but 5 will yield the leaast value of x.
Thus; 3x = 4 + 5 = 9
x = \(\frac{9}{3}\)
x = 3
WAEC Subjects
Aptitude Tests