Simplify; 2\(\frac{1}{4} \times 3\frac{1}{2} \div 4 \frac{3}{8}\)
\(\frac{5}{9}\)
1\(\frac{1}{5}\)
1\(\frac{1}{4}\)
1\(\frac{4}{5}\)
Correct answer is D
2\(\frac{1}{4} \times 3\frac{1}{2} \div 4 \frac{3}{8}\)
= \(\frac{9}{4} \times \frac{7}{2} \div \frac{35}{8}\)
= \(\frac{9}{4} \times \frac{7}{2} \div \frac{8}{35}\)
= \(\frac{9}{5}\)
= 1 \(\frac{4}{5}\)
Find the value of x for which \(32_{four} = 22_x\)
three
five
six
seven
Correct answer is C
\(32_4 = 22_x\)
\(3 \times 4^1 + 2 \times 4^o\) = \(2 \times x^1 + 2 \times x^o\)
12 + 2 x 1 = 2x + 2 x 1
14 = 2x + 2
14 - 2 = 2x
12 = 2x
x = \(\frac{12}{2}\)
x = 6
Evaluate: \((64^{\frac{1}{2}} + 125^{\frac{1}{3}})^2\)
121
144
169
196
Correct answer is C
\([64^{\frac{1}{2}} + 125^{\frac{1}{3}}]^2\) = \([\sqrt{64} + \sqrt[3] {125}]^2\)
\([8 + 5]^2\) = \([13]^2\)
= 169
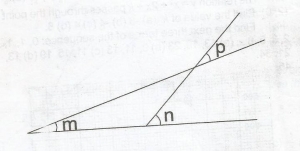
From the diagram, which of the following is true?
m + n + p = 180o
m + n = 180o
m = p + n
n = m + p
Correct answer is D
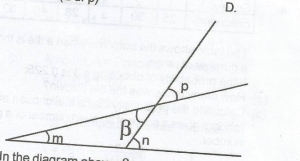
In the diagram, \(\beta\) = p(vertically opposite angles)
m + \(\beta\) = n(sum of interior opp. angles)
m + p = n
8.60m
7.83m
7.51m
7.15m
Correct answer is D
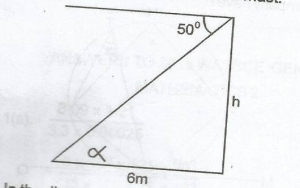
In the diagram give, \(\alpha\) 50o(alternative angles)
tan\(\alpha\) = \(\frac{h}{6}\)
h = 6tan\(\alpha\)
= 6tan 50o
= 6 x 1.1918
= 7.1508
= 7.15m (2d.p)
WAEC Subjects
Aptitude Tests