The relation y = x2 + 2x + k passes through the point (2,0). Find the value of k
- 8
- 4
4
8
Correct answer is A
Y = x2 + 2x + k (given)
y = o when x = 2
thus 0 = 22 + 2 x 2 + k
0 = 4 + 4 + k
given k = -8
\(\frac{2}{9}\)
\(\frac{5}{18}\)
\(\frac{20}{81}\)
\(\frac{5}{9}\)
Correct answer is C
n(red balls) = 5
n(blue balls) = 4
n(\(\iff\)) = 9
Hence, prob (R1, B2)
= \(\frac{5}{9} \times \frac{4}{9}\)
= \(\frac{20}{81}\)
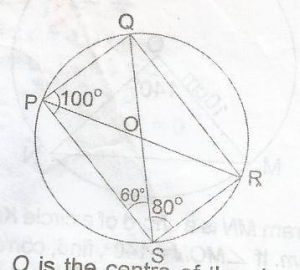
In the diagram, O is the centre of the circle, < QPS = 100o, < PSQ = 60o and < QSR. Calculate < SQR
20o
40o
60o
80o
Correct answer is A
In the diagram, < RPQ = 80o(angles in same segment)
< SPR = 100o - < RPQ
= 100 - 80
= 20o
< SQR = < SPR = 20o (same reason as above)
< SQR = 20o
Simplify \(\frac{(p - r)^2 - r^2}{2p^2 - 4pr}\)
\(\frac{1}{2}\)
p - 2r
\(\frac{1}{p - 2r}\)
\(\frac{2p}{p - 2r}\)
Correct answer is A
\(\frac{(p - r)^2 - r^2}{2p^2 - 4pr}\)
= \(\frac{(p - r)(p - r) - r^2}{2p^2 - 4pr}\)\
= \(\frac{p^2 - 2pr + r^2 - r^2}{2p(p - 2r}\)
= \(\frac{p^2 - 2pr}{2p(p - 2r)}\)
= \(\frac{p(p - 2r)}{2p(p - 2r)}\)
= \(\frac{1}{2}\)
If 20(mod 9) is equivalent to y(mod 6), find y.
1
2
3
4
Correct answer is B
First, reduce 20(mod 9) to its simplest form in mod 9; 9 x 2 + 2 = 2(mod 9)
If 2(mod 9) y(mod 6), then y = 2 by comparism
WAEC Subjects
Aptitude Tests