2.00
3.67
8.67
11
Correct answer is D
Log2(3x - 1) = 5
Log2(3x - 1) = Log225
Log2(3x - 1) = Log232
3x - 1 = 32
3x = 32 + 1 = 33
x = \(\frac{33}{3}\)
= 11
The marks of eight students in a test are: 3, 10, 4, 5, 14, 13, 16 and 7. Find the range
16
14
13
11
Correct answer is C
First, arrange the marks in order of magnitude; 3, 4, 5, 7, 10, 13, 14, 16
Hence range = 16 - 3 = 13
A fair die is thrown two times. What is the probability that the sum of the scores is at least 10?
\(\frac{5}{36}\)
\(\frac{1}{6}\)
\(\frac{5}{18}\)
\(\frac{2}{3}\)
Correct answer is B
\(\begin{array}{c|c}
& 1 & 2 & 3 & 4 & 5 & 6 \\
\hline
1 & 1,1 & 1,2 & 1,3 & 1,4 & 1,5 & 1,6 \\ \hline 2 & 2,1 & 2,2 & 2,3 & 2,4 & 2,5 & 2,6 \\ \hline 3 & 3,1 & 3,2 & 3,3 & 3,4 & 3,5 & 3,6 \\ \hline 4 & 4,1 & 4,2 & 4,3 & 4,4 & 4,5 & 4,6 \\ 5 & 5,1 & 5,2 & 5,3 & 5,4 & 5,5 & 5,6 \\ \hline 6 & 6,1 & 6,2 & 6,3 & 6,4 & 6,5 & 6,6\end{array}\)
From the table above, event space, n(E) = 6
sample space, n(S) = 36
Hence, probability sum of scores is at least 10, is;
\(\frac{n(E)}{n(S)}\)
= \(\frac{6}{36}\)
= \(\frac{1}{6}\)
Le 2,250,000.00
Le 22,700,000.00
Le 3,600,000.00
Le 4,500,000.00
Correct answer is C
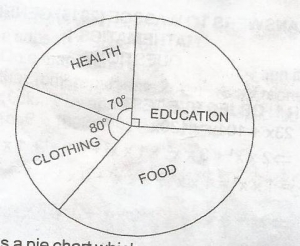
sectoral angle representing food
= 360o - (80 + 70 + 90)o
= 120o
Amount spent on food
= \(\frac{\tect{sectoral angle}}{360^o}\) x Le 10,800,000
= Le 3,600,000
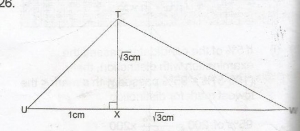
In the diagram, TX is perpendicular to UW, |UX| = 1cm and |TX| = |WX| = \(\sqrt{3}\)cm. Find UTW
135o
105o
75o
60o
Correct answer is C
In \(\Delta\) UXT, tan\(\alpha\) = \(\frac{1}{\sqrt{3}}\)
\(\alpha\) = tan-1(\(\frac{1}{\sqrt{3}}\))
= 30o
In \(\Delta\)WXT, tan\(\beta\) \(\frac{\sqrt{3}}{\sqrt{3}}\) = 1
\(\beta\) = tan-1(1) = 45o
Hence, < UTW = \(\alpha\) + \(\beta\)
= 30o + 45o = 75o
WAEC Subjects
Aptitude Tests