Simplify; \(\frac{3^{n - 1} \times 27^{n + 1}}{81^{n}}\)
32n
9
3n
3n + 1
Correct answer is B
\(\frac{3^{n - 1} \times 27^{n + 1}}{81^{n}}\)
= \(\frac{3^{n - 1} \times 3^{3(n + 1)}}{3^{4n}}\)
= 3\(^{n - 1 + 3n + 3 - 4n}\)
= 3\(^{4n - 4n - 1 + 3}\)
= 32
= 9
On a map, 1cm represent 5km. Find the area on the map that represents 100km2.
2cm2
4cm2
8cm2
8cm2
Correct answer is B
On a map, 1cm represents 5km. Then it follows that 1cm2 represents 25km2. Acm2 represents 100km2. By apparent cross-multiplication, 1cm2 x 100km2 = Acm2x 25km2
therefore A = \(\frac{100}{25}\) = 4cm2
Joseph plays football in Nigeria therefore he is a good footballer
Joseph is a good footballer therefore he is a Nigerian footballer
Joseph is a Nigerian footballer therefore he is a good footballer
Joseph plays good football therefore he is a Nigerian footballer
Correct answer is C
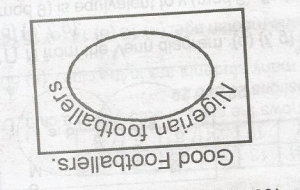
From the venn diagram, Nigeria footballers from a subset of good footballers.
90cm
135cm
180cm
225cm
Correct answer is C
d \(\alpha\) t2
d = t2 k
where k is a constant. d = 45cm, when t = 3s; thus 45 = 32 x t
k = \(\frac{45}{9}\) = 5
thus equation connecting d and t is d = 5t2
when t = 6s, d = 5 x 62
= 5 x 36
= 180cm
Simplify:(\(\frac{10\sqrt{3}}{\sqrt{5}} - \sqrt{15}\))2
75.00
15.00
8.66
3.87
Correct answer is B
Note that \(\frac{10\sqrt{3}}{\sqrt{5}} = \frac{10\sqrt{3}}{\sqrt{5}} \times - \frac{\sqrt{5}}{\sqrt{5}}\)
= \(\frac{10\sqrt{15}}{\sqrt{5}} = 2\sqrt{15}\)
hence, (\(\frac{10\sqrt{3}}{\sqrt{5}} - \sqrt{15}\))2 = (\(2\sqrt{15} - \sqrt{15}\))2
= (\(2\sqrt{15} - \sqrt{15}\))(\(2\sqrt{15} - \sqrt{15}\))
= 4\(\sqrt{15 \times 15} - 2\sqrt{15 \times 15} - 2\sqrt{15 x 15} + \sqrt{15 \times 15}\)
= 4 x 15 - 2 x 15 - 2 x 15 + 15
= 60 - 30 - 30 + 15
= 15
WAEC Subjects
Aptitude Tests