Physics Questions and Answers
If you want to learn more about the nature and properties of matter and energy or you're simply preparing for a Physics exam, these Physics past questions and answers are ideal for you.

If you want to learn more about the nature and properties of matter and energy or you're simply preparing for a Physics exam, these Physics past questions and answers are ideal for you.
26.25 cm behind the mirror
10.5 cm behind the mirror
26.25 cm in front of the mirror
10.5 cm in front of the mirror
Correct answer is B
f= -15cm (diverging mirror); u=35cm; v=?
⇒\(\frac{1}{f}\) = \(\frac{1}{u}\) + \(\frac{1}{v}\)
⇒ \(\frac{1}{-15}\) = \(\frac{1}{35}\) + \(\frac{1}{v}\)
⇒ \(\frac{1}{15}\) - \(\frac{1}{35}\) = \(\frac{1}{v}\)
⇒ \(\frac{-2}{21}\) = \(\frac{1}{v}\)
= \(\frac{-21}{2}\) = -10.5cm
∴The image is 10.5cm behind the mirror
800 Hz
600 Hz
400 Hz
200 Hz
Correct answer is A
T=800N; I=50cm=0.5m,
m=10g=0.01kg
fundamental freq: \(f_o\) =?
\(f_o\) = \(\frac{1}{21}√{T}{μ}\)
μ =\(\frac{m}{1}\)=\(\frac{0.01}{0.5}\)
⇒ \(f_o\) =\(\frac{1}{2×0.5}\)√\(\frac{800}{0.02}\)
\(f_o\) ⇒√ 40,000
⇒1st overtone = 2\(f_o\) =2×200 = 400Hz
⇒2nd overtone =3\(f_o\) =3×200=600Hz
∴3rd over tone= 4\(f_o\) =4×200=800Hz
40 kΩ
37.5 kΩ
45.5 kΩ
30 kΩ
Correct answer is B
For the combination in series;
⇒R1 = 35kΩ + 40kΩ = 75kΩ
R is combined with 75kΩ in parallel to give 25kΩ
= \(\frac{1}{R_eq}\) = \(\frac{1}{R}\) + \(\frac{1}{R}\)
= \(\frac{1}{25}\) = \(\frac{1}{R}\) + \(\frac{1}{75}\)
= \(\frac{1}{25}\) - \(\frac{1}{75}\) + \(\frac{1}{R}\)
= \(\frac{3-1}{75}\) = \(\frac{1}{R}\)
= \(\frac{2}{75}\) = \(\frac{1}{R}\)
= \(\frac{75}{2}\) = R
; R = 37.5k Ω
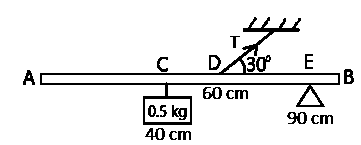
16.67N
15.67N
14.67N
18.67N
Correct answer is A
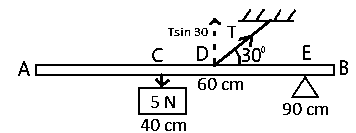
W = mg = 0.5 x 10 = 5 N
Since it's light, neglect the weight of the metre rule.
The effective tension T acting in the vertical direction = T sin 30°
From the second condition of equilibrium, sum of clockwise moments equal sum of anticlockwise moments
Taking moment at E
⇒ T sin 30° x 30 = 5 x 50
⇒ ∴T=250
T = \(\frac{250}{15}\) = 16.67N
20
250
200
500
Correct answer is D
Ep = 2.2kV = 2200V; Es=110V; Ns=25; Np=?
=\(\frac{E_p}{E_s}\) = \(\frac{N_p}{N_s}\)
= \(\frac{2200}{110}\) = \(\frac{N_p}{25}\)
=110 × Np = 2200 × 25
=\(N_p\) = \(\frac{55,000}{110}\)
∴\(N_p\) = 500 turns