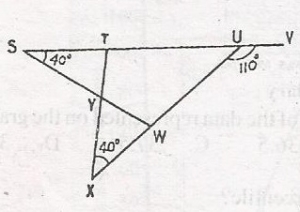
In the diagram, STUV is a straight line. < TSY = < UXY = 40o and < VUW = 110o. Calculate < TYW
150o
140o
130o
120o
Correct answer is A
< TUW = 110o = 180o (< s on a straight line)
< TUW = 180o - 110o = 70o
In \(\bigtriangleup\) XTU, < XUT + < TXU = 180o
i.e. < YTS + 70o = 180
< XTU = 180 - 110o = 70o
Also < YTS + < XTU = 180 (< s on a straight line)
i.e. < YTS + < XTU - 180(< s on straight line)
i.e. < YTS + 70o = 180
< YTS = 180 - 70 = 110o
in \(\bigtriangleup\) SYT + < YST + < YTS = 180o(Sum of interior < s)
SYT + 40 + 110 = 180
< SYT = 180 - 150 = 30
< SYT = < XYW (vertically opposite < s)
Also < SYX = < TYW (vertically opposite < s)
but < SYT + < XYW + < SYX + < TYW = 360
i.e. 30 + 30 + < SYX + TYW = 360
but < SYX = < TYW
60 + 2(< TYW) = 360
2(< TYW) = 360o - 60
2(< TYW) = 300o
TYW = \(\frac{300}{2}\) = 150o
< SYT
Similar Questions
Given that tan x = \(\frac{2}{3}\), where 0o d" x d" 90o, Find the value of 2sinx....
Simplify \(\frac{2x-1}{3}-\frac{x+3}{2}\)...
In the diagram, ST//PQ reflex angle SRQ = 198o and < RQp = 72o. Find the value of y...
In the diagram, PQR is a straight line, (m + n) = 120o and (n + r) = 100o. Find (m + r)...
A function f(x) passes through the origin and its first derivative is 3x + 2. What is f(x)? ...
Find n if log\(_{2}\) 4 + log\(_{2}\) 7 - log\(_{2}\) n = 1...
If sin \(\theta\) = \(\frac{x}{y}\) and 0o < 90o then find \(\frac{1}{tan\theta}\)...
Two ladders of length 5m and 7m lean against a pole and make angles 45° and 60° with the gro...