Calculate the area of the composite figure above.
...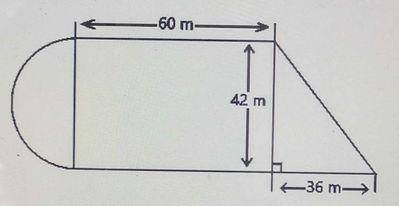
Calculate the area of the composite figure above.
6048 m\(^2\)
3969 m\(^2\)
4628 m\(^2\)
5834 m\(^2\)
Correct answer is B
Area of the composite figure = Area of semi circle + Area of rectangle + Area of triangle
Area of semi circle = \(\frac{1}{2}\pi r^2 = \frac{1}{2}\times\pi\times\frac{d^2}{4} = \frac{1}{2}\times\frac{22}{7}\times\frac{42^2}{4} = 693 m^2\)
Area of rectangle = l x b = 42 x 60 =2520 m\(^2\)
Area of triangle = \(\frac{1}{2}\times b \times h = \frac{1}{2}\times 36 \times 42 = 756 m^2\)
∴ Area of the composite figure = 693 + 2520 + 756 = 3969 m\(^2\)
Similar Questions
Simplify \(\frac{1\frac{7}{8} \times 2\frac{2}{5}}{6\frac{3}{4} \div \frac{3}{4}}\)...
If x - 3 is directly proportional to the square of y and x = 5 when y =2, find x when y = 6. ...
Convert 425 to base three numeral...
What is the equation of the line PQ?...
Form an inequality for a distance d meters which is more than 18m, but not more than 23m ...
If y = x Sin x, find \(\frac{dy}{dx}\) when x = \(\frac{\pi}{2}\)...
Evaluate \(\frac{2\sin 30 + 5\tan 60}{\sin 60}\), leaving your answer in surd form....