John was facing S35°E. If he turned 90° in t...
John was facing S35°E. If he turned 90° in the anticlockwise direction, find his new direction.
S55°E.
S35°W.
N55°E.
N35°W.
Correct answer is C
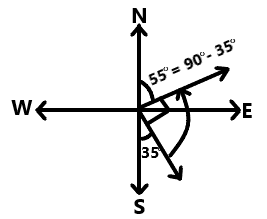
Consider |NS|
θ = 180° - (90° + 35°) (sum of angles on a straight line is 180°)
= 180° - 90° - 35°
= 90° - 35°
= 55°
∴ His new bearing is N55°E.
Similar Questions
Find n if log\(_{2}\) 4 + log\(_{2}\) 7 - log\(_{2}\) n = 1...
the graph above is a sketch of ...
The table below gives the distribution of marks obtained by a number of pupils in a class test. T...
Solve the following simultaneous equation for x. x2 + y - 5 = 0, y - 7x + 3 = 0...
The angle of a sector of a circle of diameter 8cm is 135°. Find the area of the sector [Take \(\...
Given that (2x + 7) is a factor of \(2x^2 + 3x - 14\), find the other factor...
Find the value of X if \(cos x = \frac{5}{8}\) for \(0^o\le X\le 180^o\)...