In the diagram above, PQ and XY are two concentric arc; c...
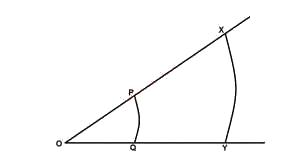
In the diagram above, PQ and XY are two concentric arc; center O, the ratio of the length of the two arc is 1:3, find the ratio of the areas of the two sectors OPQ and OXY
1:3
1:6
1:9
2:3
4:9
Correct answer is C
Let the radius of the arc PQ = r and the radius of the arc XY = R.
Length of arc PQ = \(\frac{\theta}{360} \times 2\pi r = 1\)
Length of arc XY = \(\frac{\theta}{360} \times 2\pi R = 3\)
Ratio of the arc = \(\frac{r}{R} = \frac{360 \times 2\pi \theta}{2\pi \theta \times 360 \times 3}\)
= \(\frac{1}{3}\)
Ratio of their area = \((\frac{1}{3})^2 = \frac{1}{9}\)
= 1 : 9
Similar Questions
Simplify 1 - (7/3 x 5/4) + 3/5 ...
The bearing of P from Q is x, where 270o < x < 360o. Find the bearing of Q from P...
What is the rate of change of the volume V of a hemisphere with respect to its radius r when r ...
Simplify \(\frac{x^2 - y^2}{2x^2 + xy - y^2}\)...
If P = {3, 5, 6} and Q = {4, 5, 6} then P∩Q equals ...