14.06N
13.00N
9.83N
8.26N
Correct answer is D
No explanation has been provided for this answer.
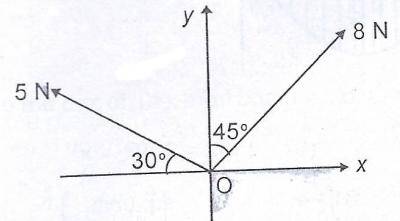
1.7N
4.5N
9.0N
13.0N
Correct answer is A
\(F = F \cos \theta + F \sin \theta\)
where \(F \cos \theta = \text{horizontal component}\)
\(F \sin \theta = \text{vertical component}\)
Horizontal component of resultant = sum of horizontal compoents of individual forces
= \(8 \cos 30 + 10 \cos 150 = 6.928 - 8.66 \approxeq - 1.7N\)
The sum, \(S_{n}\), of a sequence is given by \(S_{n} = 2n^{2} - 5\). Find the 6th term
112
67
45
22
Correct answer is D
\(S_{n} = 2n^{2} - 5\)
\(T_{n} = S_{n} - S_{n - 1}\)
\(T_{6} = S_{6} - S_{5}\)
= \((2(6^{2} - 5) - (2(5^{2} - 5) = 62 - 40 = 22\)
22m
18m
14m
10m
Correct answer is C
\(a = \frac{v - u}{t} = \frac{9 - 5}{2} = 2 ms^{-2}\)
\(s = ut + \frac{1}{2}at^{2} = 5(2) + \frac{1}{2}(2 \times 2^{2})\)
= \(14m\)
If \(2\sin^{2} \theta = 1 + \cos \theta, 0° \leq \theta \leq 90°\), find the value of \(\theta\).
90°
60°
45°
30°
Correct answer is B
\(2\sin^{2} \theta = 1 + \cos \theta\)
\(2 ( 1 - \cos^{2} \theta) = 1 + \cos \theta\)
\(2 - 2\cos^{2} \theta = 1 + \cos \theta\)
\(0 = 1 - 2 + \cos \theta + 2\cos^{2} \theta\)
\(2\cos^{2} \theta + \cos \theta - 1 = 0\)
Factorizing, we have
\((\cos \theta + 1)(2\cos \theta - 1) = 0\)
Note: In the range, \(0° \leq \theta \leq 90°\), all trig functions are positive, so we consider
\(2\cos \theta = 1 \implies \cos \theta = \frac{1}{2}\)
\(\theta = 60°\).
WAEC Subjects
Aptitude Tests