Given that cos xo = \(\frac{1}{r}\), express tan x in terms of r
\(\frac{1}{\sqrt{r}}\)
\(\sqrt{r}\)
\(\sqrt{r^2 + 1}\)
\(\sqrt{r^2 - 1}\)
Correct answer is D
cos xo = \(\frac{1}{r}\); \(\sqrt{r^2 - 1}\)
By Pythagoras r2 = 12 + x2 - 1
x = \(\sqrt{r^2 - 1}\)
tan xo = \(\sqrt{r^2 - 1}\)
= \(\sqrt{r^2 - 1}\)
Solve for x in the equation; \(\frac{3}{5}\)(2x - 1) = \(\frac{1}{4}\)(5x - 3)
zero
1
2
3
Correct answer is D
\(\frac{3}{5}\)(2x - 1) = \(\frac{1}{4}\)(5x - 3)
\(\frac{6x}{5} - \frac{3}{5} = \frac{5x}{4} - \frac{3}{4}\)
\(\frac{6x}{5} - \frac{5x}{4} = \frac{3}{5} - \frac{3}{4}\)
\(\frac{24x - 25x}{20} = \frac{12 - 15}{20}\)
\(\frac{-x}{20} = \frac{-3}{20}\)
-20x = -60
x = \(\frac{-60}{-20}\)
x = 3
If N112.00 exchanges for D14.95, calculate the value of D1.00 in naira
0.13
7.49
8.00
13.00
Correct answer is B
D14.95 = N112.00
D1.00 = \(\frac{N112}{D14.95} \times\) D1.00
= 7.49
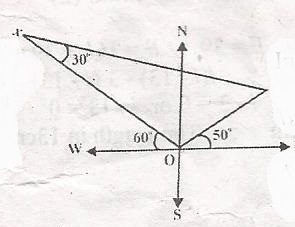
In the diagram, < WOX = 60o, < YOE = 50o and < OXY = 30o. What is the bearing of x from y?
300o
240o
190o
150o
Correct answer is A
The bearing of x from y = 270o + \(\theta\)
where \(\theta\) + 50o = y
in \(\bigtriangleup\) OXY
O + X + Y = 180o
Where O = 40o + 30o = 70o
70o + 30o + y = 180o
y + 100o = 180o
y = 180o - 100o = 30o
\(\theta\) + 50o = 80o
80o - 50o = 30o
The bearing of x from y = 270o + 30o = 300o
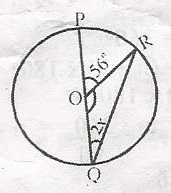
In the diagram, 0 is the centre of the circle. Find the value x
34
29
17
14
Correct answer is D
POQ in a straight line
Hence, < POQ + < QOR = 180o
56o + < QOR = 180o
< QOR = 180o - 56o
= 124o
Now, in \(\bigtriangleup\) QOR OR = OQ = Radius
< ORQ = < OQR = 2x (Base angles of an Isosceles \(\bigtriangleup\))
2x + 124 + 2x = 180o
4x + 124 = 180
4x = 180 - 124
4x = 56
x = \(\frac{56}{4}\)
x = 14o
WAEC Subjects
Aptitude Tests