
55o
45o
35o
25o
Correct answer is C
Join SR
< PRS = 90o(Angle in a semicircle)
< PRS = 55o (Angle between a chord and a tangent = Angle in the alternate segment)
< PSR + < PRS + < RSP = 180o
90v + 55o + < RSp = 180o
< RSP = 180o - 145o
= 35o
10o
11o
22o
35o
Correct answer is B
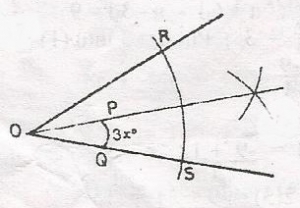
From the diagram, OP bisects < ROS
< POS = \(\frac{1}{2}\) < ROS = \(\frac{1}{2}\) x 66o
3x = 33o
x = \(\frac{33^o}{3}\)
= 11o
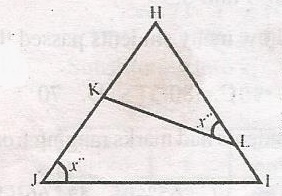
\(\frac{KL}{JI}\)
\(\frac{HK}{JK}\)
\(\frac{JI}{KL}\)
\(\frac{HK}{LK}\)
Correct answer is A
\(\bigtriangleup\) is similar to \(\bigtriangleup\) HIJ
< HKL = HJI = xo
Hence, \(\frac{LH}{JH} = \frac{KH}{JH} \frac{KL}{IJ}\)
\(\frac{LH}{JH} = \frac{KL}{JI}\)
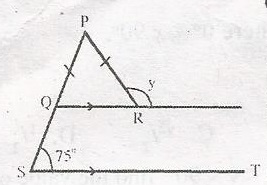
In the diagram, QR//ST, /PQ/ = /PR/ and < PST = 75o. Find the value of y
105o
110o
130o
150o
Correct answer is A
In \(\bigtriangleup\) PQR,
Q = S = 75o (Corresponding angle)
R = Q = 75o (Base angles of an isosceles \(\bigtriangleup\))
But, y + 75o = 180o (Sum of angles in a straight line)
y = 180 - 75
y = 105o
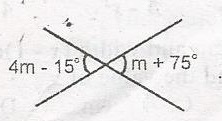
What is the value of m in the diagram?
20o
30o
40o
50o
Correct answer is B
4m - 15o = m + 75o
(Vertically opposite angles are equal)
4m - m = 75 + 15
3m = 90
m = \(\frac{90}{3}\)
m = 30o
WAEC Subjects
Aptitude Tests