19.5cm2
15.0cm2
13.0cm2
9.3cm2
Correct answer is B
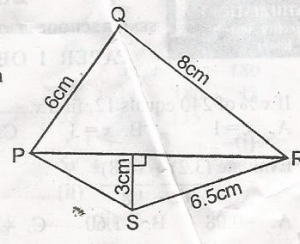
Perimeter of \(\bigtriangleup\) PQR = PQ + QR + PR
24cm = 6cm + 8cm = PR
24 = 14 + PR
PR = 24 - 14 = 10cm
Area of \(\bigtriangleup\) PRS = \(\frac{1}{2} \times 10 \times 3cm^3\)
= 15cm3
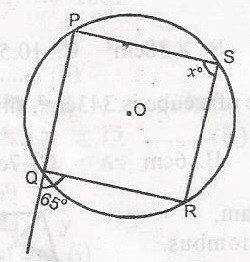
25o
65o
115o
130o
Correct answer is B
x = 65o (An interior angle of a cyclic quadrilateral = opposite exterior angle).
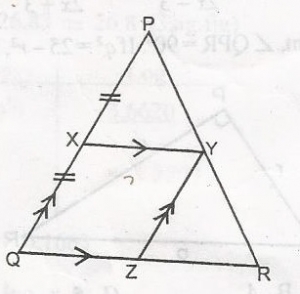
1:2
2:1
1:2
3:1
Correct answer is B
From the diagram, XYZQ is a parallelogram. Thus, |YZ| = |XQ| = |PX|; \(\bigtriangleup\)PXY, Let the area of XYZQ = A1, the area of \(\bigtriangleup\)PXY
= Area of \(\bigtriangleup\)YZR = A2
Area of \(\bigtriangleup\)PQR = A = A1 + 2A2
But from similarity of triangles
\(\frac{\text{Area of PQR}}{\text{Area of PXY}} = (\frac{PQ}{PX})^2 = (\frac{QR}{XY})^2\)
\(\frac{A}{A_2} = (\frac{2}{1})^2 = \frac{2}{1}\)
A = 4A2 But, A = A1 + 2A
A1 = 4A2 - 2A2
A1 = 2A2
\(\frac{A_1}{A_2}\) = 2
A1:A2 = 2:1
Area of XYZQ:Area of \(\bigtriangleup\)YZR = 2:1
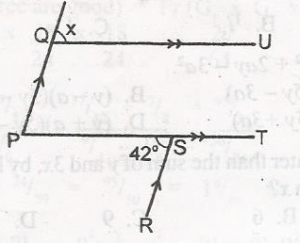
In the diagram, PQ//RS, QU//PT and < PSR = 42o. Find angle x.
84o
48o
42o
32o
Correct answer is C
From the diagram, < QPS = xo (Corresponding angles)
Also, < QPS = < PSR(Alternate angles)
x = 42o
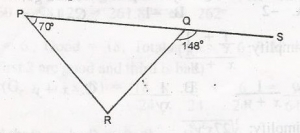
In the figure shown, PQs is a straight line. What is the value of < PRQ?
128o
108o
98o
78o
Correct answer is D
< QPR + < PRQ = < RQS
(Sum of two interior angles of a triangle = Opposite exterior angles)
70o + < PRQ = 148
< PRQ = 148o - 70o
= 78o
WAEC Subjects
Aptitude Tests