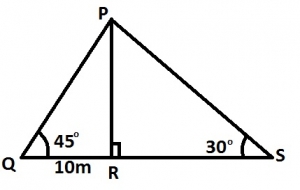
In the diagram, |QR| = 10cm, PR⊥QS, angle PSR = 30° and angle PQR = 45°. Calculate in meters |QS|
\(10(1+\sqrt{3})\)
\(20\sqrt{3}\)
\(10\sqrt{3}\)
\((10+\sqrt{3})\)
Correct answer is A
In \(\Delta\) PQR,
\(\tan 45 = \frac{PR}{10} \implies PR = 10 \tan 45\)
= 10m
In \(\Delta\) PRS,
\(\tan 30 = \frac{10}{RS} \implies RS = \frac{10}{\tan 30}\)
= \(\frac{10}\{\frac{1}{\sqrt{3}}\)
= \(10\sqrt{3}\)
PS = \(10 + 10\sqrt{3}\)
= \(10(1 + \sqrt{3}) cm\)
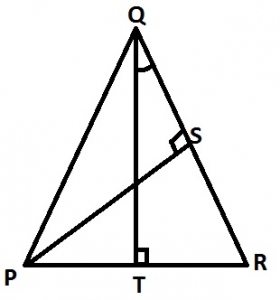
∠PQT
∠SRP
∠PQR
∠SPR
Correct answer is D
No explanation has been provided for this answer.
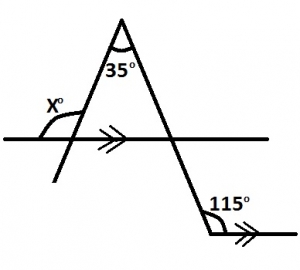
In the diagram, calculate the value of x
35o
80o
100o
115o
Correct answer is C
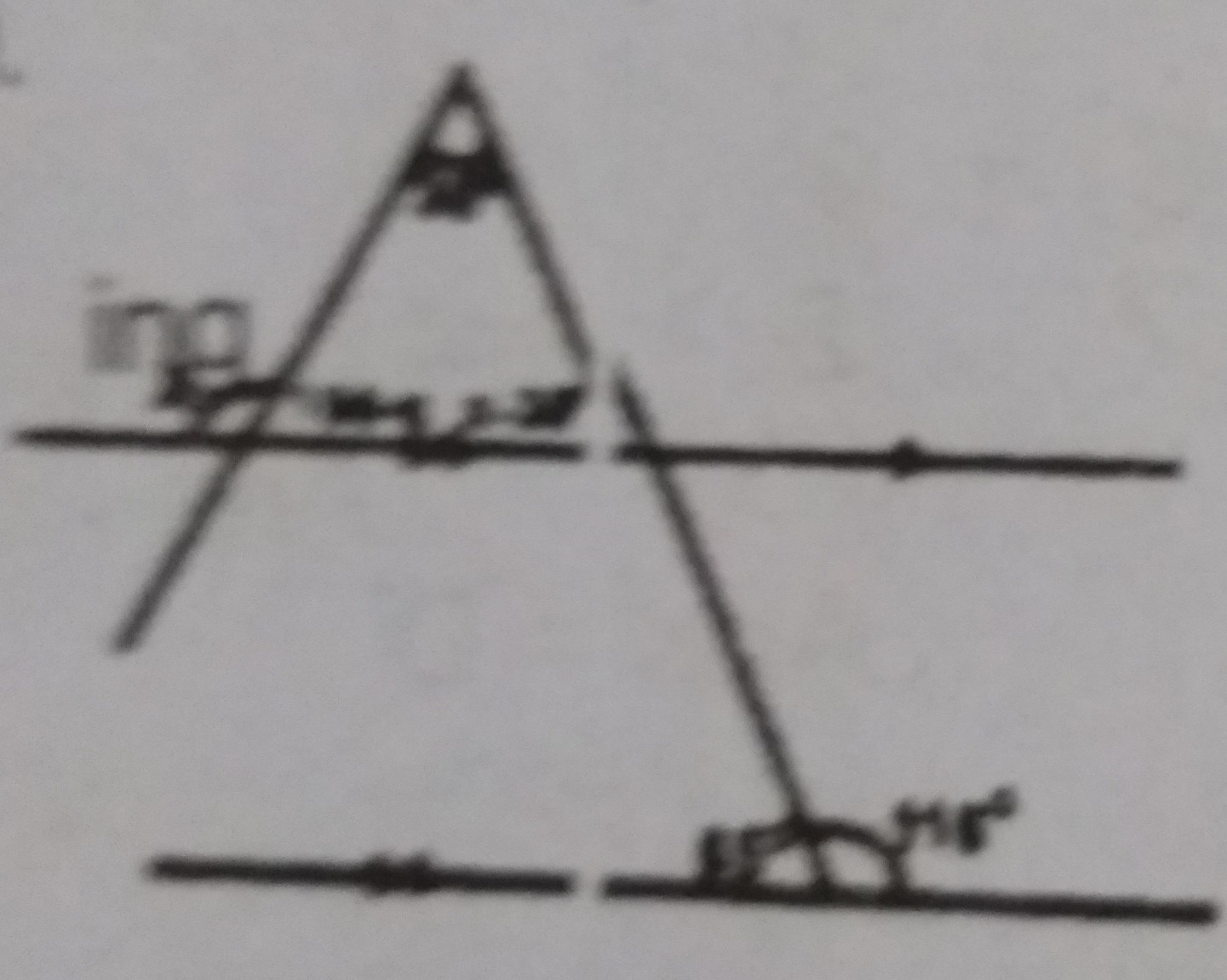
x - 35° = 65° (corresponding angles)
x = 65° + 35° = 100°
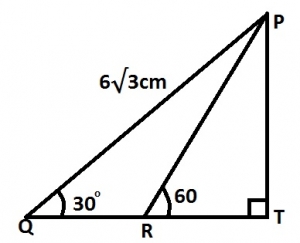
0.3cm
\(\frac{\sqrt{3}}{2}cm\)
3cm
\(3\sqrt{3}cm\)
Correct answer is C
In \(\Delta\) QPT,
\(\frac{PT}{6\sqrt{3}} = \sin 30°\)
PT = \(6\sqrt{3} \times \frac{1}{2} = 3\sqrt{3} cm\)
In \(\Delta\) RPT,
\(\frac{PT}{RT} = \tan 60°\)
\(\frac{3\sqrt{3}}{RT} = \tan 60°\)
\(RT = \frac{3\sqrt{3}}{\sqrt{3}} = 3 cm\)
If q oranges are sold for t Naira, how many oranges can be bought for p naira?
\(\frac{p}{2}t\)
\(\frac{qt}{p}\)
\(\frac{q}{pt}\)
\(\frac{pq}{t}\)
Correct answer is D
q oranges = t naira
1 naira = \(\frac{q}{t}\)
p naira = \(p(\frac{q}{t})\)
= \(\frac{pq}{t}\) oranges
WAEC Subjects
Aptitude Tests