112
90
68
22
Correct answer is C
No explanation has been provided for this answer.
Given that sin x = 3/5, 0 ≤ x ≤ 90, evaluate (tanx + 2cosx)
2\(\frac{11}{20}\)
\(\frac{11}{20}\)
2\(\frac{7}{20}\)
\(\frac{1}{20}\)
Correct answer is B
Sin x = \(\frac{opp}{hyp}\)
sinx = \(\frac{3}{5}\)
using Pythagoras' theorem
hyp\(^2\) = opp\(^2\) + adj\(^2\)
adj\(^2\) = 5\(^2\) - 3\(^2\) = 25 - 9
adj\(^2\) = 16
adj = √ 16
adj = 4.
tanx = \(\frac{opp}{adj}\)
= \(\frac{3}{4}\)
cosx = \(\frac{adj}{hyp}\)
= \(\frac{4}{5}\)
(tanx + 2cosx) = \(\frac{3}{4}\) + 2(\(\frac{4}{5}\))
= \(\frac{15 + 32}{20}\)
= \(\frac{47}{20}\) or
2 \(\frac{7}{20}\)
341.98cm\(^2\)
276.57cm\(^2\)
201.14cm\(^2\)
477.71cm\(^2\)
Correct answer is A
Where l\(^2\) = h\(^2\) + r\(^2\)
l\(^2\) = 11\(^2\) + 8\(^2\)
l = √185
l = 13.60cm
The formula of CSA of Cone is πrl
\(\frac{22}{7}\) * 8 * 13.60
= 341.979 or 341.98 (2d.p)
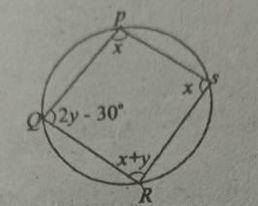
In the diagram, PQRS is a circle. find the value of x.
50°
30°
80°
100°
Correct answer is A
Opp. angles in a cyclic quadrilateral always add up to 180°
∠P + ∠R & ∠Q + ∠S = 180
x + x+y = 180
2x + y = 180... i
2y - 30 + x = 180
2y + x = 180 + 30
x + 2y = 210 ... ii
Elimination method:
(2x + y = 180) * 1 --> 2x + y = 180
(x + 2y = 210) * 2 --> 2x + 4y = 420
Subtracting both equations
- 3y = - 240
y = 80°
using eqn i
2x + y = 180
2x + 80 = 180
2x = 100
x = 50°
find the first quartile of 7,8,7,9,11,8,7,9,6 and 8.
8.5
7.0
7.5
8.0
Correct answer is B
Rearrange data in increasing order: 6,7,7,7,8,8,8,9,9 and 11
First quartile (ungrouped data) = \(\frac{n}{4}\)th value
= \(\frac{10}{4}\)
= 2.5th value
= \(\frac{7 + 7}{2}\)
= 7.0
WAEC Subjects
Aptitude Tests