Find the quadratic equation whose roots are \(\frac{2}{3} and \frac{- 3}{4}\)
\(12y^2 - y - 6 = 0\)
\(12y^2 - y + 6 = 0\)
\(12y^2 + y - 6 = 0\)
\(y^2 + y - 6 = 0\)
Correct answer is C
Let p = \(\frac{2}{3}\) and q = \(\frac{- 3}{4}\)
using (y - p)(y - q) = 0
= ( y - \(\frac{2}{3})\)( y - (\(\frac{- 3}{4})) = 0\)
= (\( y - \frac{2}{3})( y + \frac{3}{4})\) = 0
\( y^2 + \frac{3}{4}y - \frac{2}{3}y - \frac{6}{12} = 0 \)
\( y^2 + \frac{1}{12}y - \frac{1}{2}\) = 0
= multiply through by the l. c. m of 3 and 4 = 12
∴ the quadratic equation is \(12y^2 + y - 6 = 0\)
Solve: \(log_3 x + log_3 (x - 8) = 2\)
8
6
9
7
Correct answer is C
\(log_3 x + log_3 (x - 8) = 2\)
\(log_3 x(x - 8) = log_39\) since 2 = \(log_39\)
\(log_3\) cancels out
⇒ x(x - 8) = 9
⇒ \(x^2 - 8x = 9\)
⇒ \(x^2 - 8x - 9 = 0\)
⇒ \(x^2 - 9x + x - 9 = 0\)
⇒ x(x - 9) + 1(x - 9) = 0
⇒ (x - 9)(x + 1) = 0
⇒ x = 9 or x = -1
Since we can't have a log of negative numbers,
∴ x = 9.
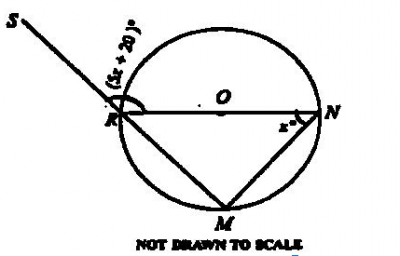
In the diagram, NR is a diameter, ∠MNR = x° and, ∠SRN = (5x + 20)°. Find the value of 2x.
\(42^0\)
\(35^0\)
\(20^0\)
\(90^0\)
Correct answer is B
∠RMN = 90° (angles in a semicircle is a right angle)
∠SRN = ∠RMN + ∠MNR (ext. angle of a ∆ is equal to the sum of two opp. int. angles)
⇒ 5x + 20 = 90 + x
⇒ 5x - x = 90 - 20
⇒ 4x = 70
x = \(\frac{70}{4}\)
= 17.4°
therefore, 2x = 2\(\times17.5\) = 35°
The price of a shoe was decreased by 22%. If the new price is $27.3. what is the original price.
$62.30
$42.30
$72.00
$35.00
Correct answer is D
Let x = original price
A decrease of 22% = (100-22)% = 78% of the original price.
78% of x = 27.30
= \(\frac{78x}{100} = 27.30\)
78x = 2730
then, x = \(\frac{2730}{78}\)
x = 35
Therefore, the original price of the shoe was $35.00.
Write the name of a triangle with the vertices (1, -3), (6, 2) and (0,4)?
Scalene triangle
Isosceles triangle
Right -angle triangle
Equilateral triangle
Correct answer is B
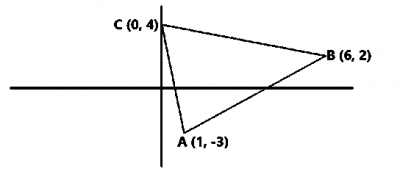
Let A = (1, -3), B = (6, 2) and C = (0,4)
\(d =\sqrt{ (y_2 - y_1)^2 + (x_2 - x_1)^2}\)
|AB| = \(\sqrt{(2 - (-3))^2 + (6 - 1)^2}\)
= \(\sqrt{(2 + 3)^2 + (6 - 1)^2}\)
= \(\sqrt{5^2 + 5^2}\)
= \(\sqrt{25 + 25}\)
= \(\sqrt50\)
= 5\(\sqrt2\) units
|BC| = \(\sqrt{(4 - 2)^2 + (0 - 6)^2}\)
= \(\sqrt{2^2 + (-6)^2}\)
= \(\sqrt{4 + 36}\)
= \(\sqrt40\)
= 2\(\sqrt10\) units
|AC| = \(\sqrt{(4 - (-3)^2 + (0 - 1)^2}\)
= \(\sqrt{(4 + 3)^2 + (0 - 1)^2}\)
= \(\sqrt{7^2 + (-1)^2}\)
= \(\sqrt{49 + 1}\)
= \(\sqrt50\)
= 5\(\sqrt{2}\) units
Since two sides are equal (|AB| = |AC|), then the triangle is Isosceles.
WAEC Subjects
Aptitude Tests