The length of a rectangle is 10 cm. If its perimeter is 28 cm, find the area
30cm\(^2\)
40cm\(^2\)
60cm\(^2\)
80cm\(^2\)
Correct answer is B
perimeter = 2( length + breadth)
→ 28 = 2 (10+ b)
14 - 10 = b
b = 4
Area = length x breadth
10 x 4 → 40cm\(^2\)
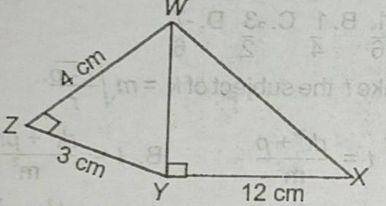
In the diagram, ∠ZWZY and WYX are right angles. Find the perimeter of WXYZ.
30cm
32cm
35cm
37cm
Correct answer is B
In ΔWYZ:
hyp\(^2\) = adj\(^2\) + opp\(^2\)
hyp\(^2\) =3\(^2\) + 4\(^2\) → 9 + 16
hyp\(^2\) = 25
hyp = 5
In ΔWXY:
hyp\(^2\) = adj\(^2\) + opp\(^2\)
hyp\(^2\) = 12\(^2\) + 5\(^2\) = 144 +25
hyp\(^2\) = 169
hyp = 13
the perimeter of WXYZ. = 3+4+12+13 → 32cm
Use the passage below to answer the question below
Human trafficking
Inconsiderate government
Lack of family planning
Non-payment of salaries
Correct answer is A
No explanation has been provided for this answer.
126.5cm\(^2\)
165.0cm\(^2\)
212.0cm\(^2\)
214.5cm\(^2\)
Correct answer is D
The surface area of an open-top cylinder = πr(r + 2h),
where 'r' is the radius and 'h' is the height of the cylinder.
= \(\frac{22}{7}\) * 3.5 (3.5 + 2 * 8)
= 11 (3.5 + 16) → 11 (19.5)
= 214.5cm\(^2\)
3.611m
4.521m
4.792m
3.962m
Correct answer is C
Sin θ = \(\frac{opp}{hyp}\) → \(\frac{x}{6}\)
cross multiply:
sin53º * 6 = x
0.7986 * 6
4.792m
WAEC Subjects
Aptitude Tests