32o
45o
60o
75o
Correct answer is A
In a school with students' population 810, the sectoral angle for a class of 72 students is
= \(\frac{72}{810}\) x 360º
= 32º
400.00m
692.82m
923.76m
1,600.99m
Correct answer is D
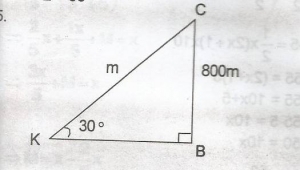
In \(\bigtriangleup\)KBC, sin 30 = \(\frac{800}{IKCI}\)
IKCL = \(\frac{800}{sin30^o}\)
= \(\frac{800}{0.5}\)
= 1600m
PQRT is square. If x is the midpoint of PQ, Calculate correct to the nearest degree, LPXS
53o
55o
63o
65o
Correct answer is C
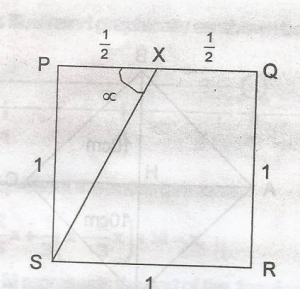
In the diagram given,
tan\(\alpha\) = \(\frac{1}{0.5}\) = 2
\(\alpha\) = tan - 1(2) = 63.43o
= 63o
1
2
3
4
Correct answer is B
Ler: (x1, y1) = (0, 3)
(x2, y2) = (\(\frac{5}{4}, \frac{11}{2}\))
Using gradient, m = \(\frac{y_2 - y_2}{x_2 - x_1}\)
= \(\frac{\frac{11}{2} - 3}{\frac{5}{4} - 0}\)
= \(\frac{11 - 6}{2} + \frac{5}{4}\)
= \(\frac{5}{} + \frac{5}{4}\)
= \(\frac{5}{2} \times \frac{4}{5}\)
= 2
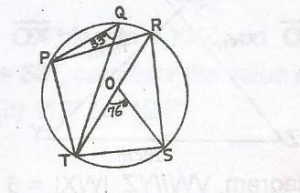
73o
67o
57o
37o
Correct answer is C
In the diagram given, < PRT = 3\(^o\) (Change in same segment)
< TPR = 90\(^o\) (angle in a semicircle)
Hence, < PTR = 180\(^o\) - (90 + 33)\(^o\)
= 180\(^o\) - 123\(^o\)
= 57\(^o\)
WAEC Subjects
Aptitude Tests