Let U = {1, 2, 3, 4}, P = {2, 3} and Q = {2, 4}. What is (P∩Q)'?
(1, 2, 3)
(1, 3, 4)
(2, 3)
(1, 3)
(1, 4)
Correct answer is B
U = {1,2,3,4}; P = {2,3}; Q = {2,4}; P∩Q = {2} (P∩Q)' = {1,3,4}
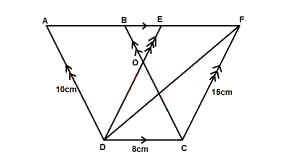
In the diagram above , |AD| = 10cm, |DC| = 8cm and |CF| = 15cm. Which of the following is correct?
Area BCF = Area DCF
Area ADE = Area ADF
Area ADE = Area DCFE
Area CBF = Area DABC
Area DABO = Area CFEO
Correct answer is E
No explanation has been provided for this answer.
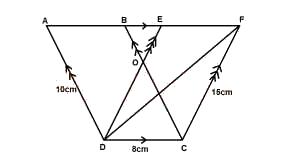
24cm2
48cm2
80cm2
96cm2
120cm2
Correct answer is B
Area of \(\Delta\)DCF = 24cm2
Area of Quad= 2 x 24 = 48cm2
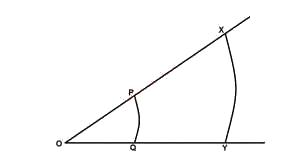
1:3
1:6
1:9
2:3
4:9
Correct answer is C
Let the radius of the arc PQ = r and the radius of the arc XY = R.
Length of arc PQ = \(\frac{\theta}{360} \times 2\pi r = 1\)
Length of arc XY = \(\frac{\theta}{360} \times 2\pi R = 3\)
Ratio of the arc = \(\frac{r}{R} = \frac{360 \times 2\pi \theta}{2\pi \theta \times 360 \times 3}\)
= \(\frac{1}{3}\)
Ratio of their area = \((\frac{1}{3})^2 = \frac{1}{9}\)
= 1 : 9
Find the area of an equivalent triangle of side 16cm
64√3cm2
72√3cm2
96cm2
128√3cm2
128cm2
Correct answer is A
Area = 1/2 x 16 x 16sin60o = 64√3cm2
WAEC Subjects
Aptitude Tests