Solve, correct to three significant figures, (0.3)\(^x\) = (0,5)\(^8\)
4.61
4.606
0.461
0.0130
Correct answer is A
(0,3)\(^x\) = (0.5)\(^8\)
xlog 0,3 = 9 log 0.5
x = \(\frac{8 \log 0.5}{\log 0.3}\)
= 4.606
70 kg ms\(^{-1}\)
55 kg ms\(^{-1}\)
50 kg ms\(^{-1}\)
35 kg ms\(^{-1}\)
Correct answer is A
Change in momentum
= F x t = 35N x 2
= 70kg ms\(^{-1}\)
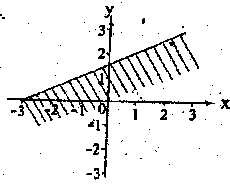
Which of these inequalities is represented by the shaded portion of the graph?
2y + x - 3 < 0
2y - x - 3 < 0
2y - x + 3 < 0
2y + x +3 < 0
Correct answer is B
(0, 1.5), (-3, 0)
m = \(\frac{0 - 1.5}{-3, 0}\) = 0.5
0.5 = \(\frac{y - 1.5}{-3.0}\) = 0.5
y = 0.5x + 1.5
2y = x + 3
2y - x - 3 < 0
Find the constant term in the binomial expansion of (2x\(^2\) + \(\frac{1}{x^2}\))\(^4\)
10
12
24
42
Correct answer is B
6(2x\(^2\))\(^2\) (\(\frac{1}{x^2}\))\(^2\)
= 6 x 2
= 12
12m
16m
64m
96m
Correct answer is B
V = 3t\(^2\) - 6t
\(\frac{ds}{dt} = 3t^2 - 6t\)
s = \(\int 3t^2 - 6t\)
s = \(\frac{3t^3}{3} - \frac{6t^2}{2} + k\)
s = t\(^3\) - 3t\(^2\) + k
s = 0, t = 0
s = t\(^3\) - 3t\(^2\)
s = 4\(^3\) - 3t\(^2\)
s = 4\(^3\) - 3(4)\(^2\)
= 64 - 48 = 16m
WAEC Subjects
Aptitude Tests