Find the quadratic equation whose roots are 3 and \(\frac{2}{3}\).
x2 - 11 / 3x + 6 = 0
x2 - 11x + 6 = O
3x2 - 11x + 2 = O
3X2 - 11x – 2 = 0
3x2 - 11x + 6 = 0
Correct answer is E
x = 3; x = \(\frac{2}{3}\).
(x - 3)(x - \(\frac{2}{3}\)) = 0
\(x^2 - \frac{2x}{3} - 3x + 2 = 0\)
\(x^2 - \frac{11x}{3} + 2 = 0\)
\(3x^2 - 11x + 6 = 0\)
Which of the following is not a factors of 2p\(^2\) - 2?
2
p - 1
p + 1
2p - 2
2p + 1
Correct answer is E
2p\(^2\) - 2
2(p\(^2\) - 1)
= 2(p + 1)(p - 1)
x2 - 2 = 0
x2 - 4 = 0
x2 + 6 = 0
X2 - X – 2 = 0
x2 - x + 4 = 0
Correct answer is B
The points of intersection of the curve and the line are at x = -2 and x = 2.
\(\therefore\) (x + 2) = 0; (x - 2) = 0.
(x + 2)(x - 2) = 0
\(x^2 - 4 = 0\)
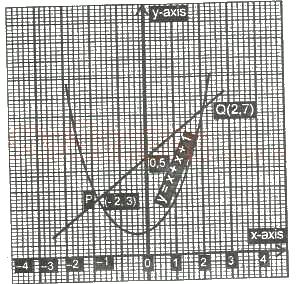
What is the equation of the line PQ?
y = x - 5
y = x + 3
y = x + 5
y = 2x + 3
y = 2x - 3
Correct answer is C
The points P(-2, 3) and Q(2, 7) are on the line.
Gradient of the line = \(\frac{7 - 3}{2 - (-2)}\)
= \(\frac{4}{4}\)
= 1
y = x + b
To find the intercept, we have
7 = 2 + b or 3 = -2 + b.
Solving for b, we get b = 5.
\(\therefore\) The line is y = x + 5.
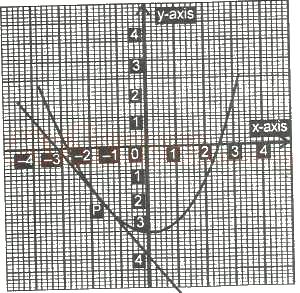
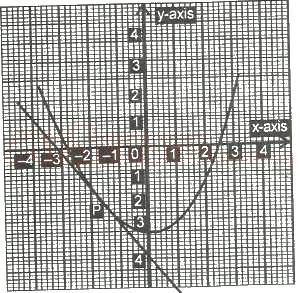
In the graph above, the gradient of the curve at the point P is
-11 3
-3 4
3/7
3/4
11 3
Correct answer is A
-1-(-3)/-2-(-0.5) = 2/-1.5 = 20/-15 = -113
WAEC Subjects
Aptitude Tests