Evaluate \(\frac{0.009}{0.012}\), leaving your answer in standard form.
7.5 x 102
7.5 x 101
7.5 x 10-1
7.5 x 10-2
7.5 x 10-3
Correct answer is C
\(\frac{0.009}{0.012}\)
=\(\frac{0.009}{0.012}\) = \(\frac{9}{12}\) = 0.75
=\(7.5 \times 10^{-1}\)
(35-2b)(b-1)
(7+b)(5-b)
(3+7b)(5-b)
(35-b)(3b+7)
(7+b)(5+b)
Correct answer is B
35 - 2b - b 2;
35 - 7b + 5b - b 2
7(5 - b) + 5(5 - b)
(7 + b)(5 - b)
Evaluate, using logarithm tables \(\frac{5.34 \times 67.4}{2.7}\)
1.332
13.32
133.2
1332
13.320
Correct answer is C
| No | Log |
| 5.34 | 0.7275 + |
| 67.4 | 1.8287 |
| 2.5562 - | |
| 2.7 | 0.4314 |
| Antilog = 133.2 | 2.1248 |
\(\therefore \frac{5.34 \times 67.4}{2.7} = 133.2\)
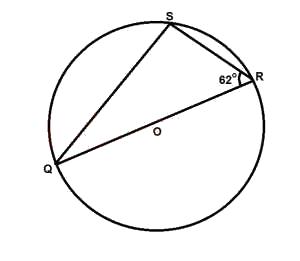
In the diagram O is the center of the circle, if ∠QRS = 62o, find the value of ∠SQR.
14o
28o
31o
45o
90o
Correct answer is B
< QSR = 90° (angle in a semi-circle)
\(\therefore\) < SQR = 180° - (90° + 62°)
= 28°
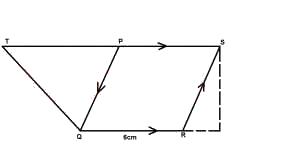
39cm2
28cm2
24cm2
21cm2
19cm2
Correct answer is B
Area of \(\Delta\)QST = 52cm\(^2\); height = 8cm
b=base length; but A = 1/2 b x h
=52=1/2 x b x 8cm = 104 =8b
b=104/8 = 13cm; ST= 13cm; PS = 6cm
TP = 13 - 6 = 7cm;
area of \(\Delta\)QST = 1/2 b x h
= 1/2 x 7 x 8/1 = 28cm\(^2\)
WAEC Subjects
Aptitude Tests