Which of the following is used to determine the mode of a grouped data?
Bar chart
Frequency polygon
Ogive
Histogram
Correct answer is D
No explanation has been provided for this answer.
Make K the subject of the relation T = \(\sqrt{\frac{TK - H}{K - H}}\)
K = \(\frac{H(T^2 - 1)}{T^2 - T}\)
K = \(\frac{HT}{(T - 1)^2}\)
K = \(\frac{H(T^2 + 1)}{T}\)
K = \(\frac{H(T - 1)}{T}\)
Correct answer is A
T = \(\sqrt{\frac{TK - H}{K - H}}\)
Taking the square of both sides, give
T2 = \(\frac{TK - H}{K - H}\)
T2(K - H) = TK - H
T2K - T2H = TK - H
T2K - TK = T2H - H
K(T2 - T) = H(T2 - 1)
K = \(\frac{H(T^2 - 1)}{T^2 - T}\)
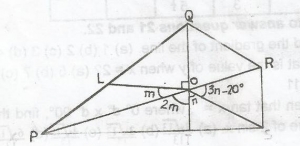
35o
40o
55o
60o
Correct answer is A
In the diagram, QOR + 2m(vertically opposite angles)
So, m + 90° + 2m = 180°
(angles on str. line)
3m = 180° - 90°
3m = 90°
m = \(\frac{90^o}{3}\)
= 30°
substituting 30° for m in
2m + 4n = 200° gives
2 x 30° + 4n = 200°
60° + 4n = 200°
4n = 200° - 60°
= 140°
n = \(\frac{140°}{4}\)
= 35°
\(\frac{1}{3}\)
\(\frac{2}{3}\)
1\(\frac{1}{3}\)
1\(\frac{2}{3}\)
Correct answer is C
\(\frac{\sqrt{2} + \sqrt{3}}{\sqrt{3}}\) = \(\frac{\sqrt{2} + \sqrt{3}}{\sqrt{3}}\) x \(\frac{\sqrt{3}}{\sqrt{3}}\)
= \(\frac{\sqrt{2} \times \sqrt{3} + \sqrt{3} \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}}\)
= \(\frac{\sqrt{6} + 3}{3}\)
= \(\frac{3 + \sqrt{6}}{3}\)
= Hence, (m + n) = 1 + \(\frac{1}{3}\)
= 1\(\frac{1}{3}\)
Tom will be 25 years old in n years' time. If he is 5 years younger than Bade's present age.
(30 - n)years
(20 - n)years
(25 - n)years
(30 + n)years
Correct answer is A
Let Tom's present agr be x.
Then x = 25 - n
If Tom is 5 years younger than Bade, then Bade's present age is x + 5 = 25 - n + 5
= (30 - n)
WAEC Subjects
Aptitude Tests