Given that (2x + 7) is a factor of \(2x^2 + 3x - 14\), find the other factor
x + 2
2 - x
x - 2
x + 1
Correct answer is C
\(2x^2 + 3x - 14\)
\(2x^2 + 7x - 4x - 14\)
\(x(2x + 7) - 2(2x + 7)\)
= \((x - 2)(2x + 7)\)
The other factor = (x - 2).
\(\frac{1}{18}\)
\(\frac{8}{81}\)
\(\frac{9}{2}\)
8
Correct answer is D
\(x \propto \frac{1}{y}\)
\(x = \frac{k}{y}\)
\(\frac{2}{3} = \frac{k}{9}\)
\(3k = 18 \implies k = 6\)
\(x = \frac{6}{y}\)
When y = \(\frac{3}{4}\),
x = \(\frac{6}{\frac{3}{4}}\)
= \(\frac{6 \times 4}{3}\)
= 8
Given that \(27^{(1+x)}=9\) find x
-3
\(\frac{-1}{3}\)
\(\frac{5}{3}\)
2
Correct answer is B
\(27^{(1+x)}=9\\
3^{3(1+x)}=3^2\\
3(1+x)=2\\
3+3x = 2\\
3x = -1
x = \frac{-1}{3}\)
Given that \(x = -\frac{1}{2}and \hspace{1mm} y = 4 \hspace{1mm} evaluate \hspace{1mm} 3x^2y+xy^2\)
-5
-1
4
11
Correct answer is A
\(x = -\frac{1}{2}, y = 4\\
3x^2y + xy^2\\
3\left[-\frac{1}{2}\right]^2 \times 4 \times + \left(\frac{-1}{2}\right)(4)^2\\
3\times \frac{1}{4} \times 4 -\frac{1}{2} \times 16\\
3-8 = -5\)
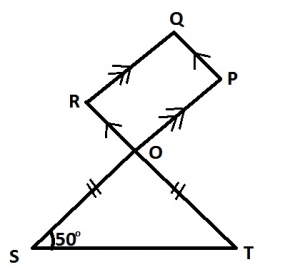
160o
140o
120o
100o
Correct answer is D
< T = < S = 50° (OS = OT)
< SOT = 180° - 2(50°) = 80°
< ROP = 80° (vertically opposite angle)
\(\therefore\) < OPQ = 180° - 80° = 100° (adjacent angles)
WAEC Subjects
Aptitude Tests