\(2311_5\)
\(1131_5\)
\(1311_5\)
\(2132_5\)
Correct answer is C
\(413_7\) to base 5
convert first to base 10
\(417_7 = 4 × 7^2 + 1 × 7^1 + 3 × 7^0\)
= 4 × 49 + 1 × 7 + 3 × 1
= 196 + 7 + 3
= \(206_{10}\)
convert this result to base 5
| 5 | 206 |
| 5 | 41R1 |
| 5 | 8R1 |
| 5 | 1R3 |
| 0R1 |
\(∴ 413_7 = 1311_5\)
For what value of x is \(\frac{ x^2 + 2 }{ 10x^2 - 13x - 3}\) is undefined?
\(\frac{1}{5}, \frac{3}{2}\)
\(\frac{-1}{5}, \frac{3}{2}\)
\(\frac{1}{5}, \frac{-3}{2}\)
\(\frac{-1}{5}, \frac{-3}{2}\)
Correct answer is B
The fraction \(\frac{ x^2 + 2 }{ 10x^2 - 13x - 3}\) is undefined when the denominator is equal to zero
\(then 10x^2 - 13x - 3 = 0\)
by factorisation, \(10x^2 - 13x - 3\) = 0 becomes \( 10x^2 - 15x +2x -3\) = 0
\(5x(2x - 3) + 1(2x - 3) = 0\)
\((5x + 1)(2x - 3) = 0\)
\(then, x = \frac{-1}{5}\) or \(\frac{3}{2}\)
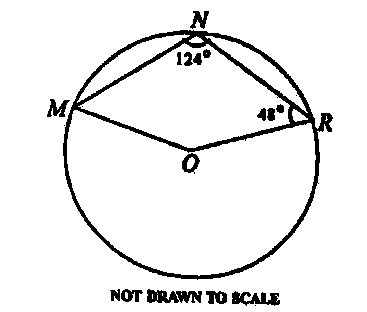
\(58^0\)
\(64^0\)
\(48^0\)
\(76^0\)
Correct answer is D
Reflex ∠MOR = 2 × 124° = 248° (angle at the centre is twice the angle at the circumference)
∠MOR = 360° - 248° = 112° (sum of angle at a point is 360°)
∠OMN = 360° - (124°+ 48° + 112°) (sum of angles in a quadrilateral is 360°)
= 360° - 284°
∴ ∠OMN = 76°
One-third of the sum of two numbers is 12, twice their difference is 12. Find the numbers.
22 and 14
20 and 16
21 and 15
23 and 13
Correct answer is C
Let the two numbers be x and y
\(\frac{1}{3}( x + y) = 12\)
then x + y = 36 ..........i
2( x - y) = 12
x - y = 6 ............ii
add equations i and ii
2x = 42
x = 21, put x = 21 into equation i
x + y = 36
21 + y = 36
y = 36 - 21 = 15
therefore the numbers are 21 and 15
147.78m
104.05m
161.87m
192.91m
Correct answer is B
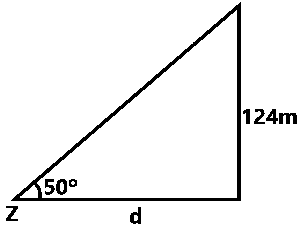
From the diagram above; Tan\(\theta = \frac{opp}{adj}\)
tan50° = \(\frac{124}{d}\)
d = \(\frac{124}{tan50}\)
therefore, d = 104.05m
WAEC Subjects
Aptitude Tests