24\(^o\)
42\(^o\)
48\(^o\)
66\(^o\)
Correct answer is A
RSP = 90 < substance in semi a circle
RPS = 180 - (90 + 24)
= 180 - (114)
= 66
TPS = 180 - 66
= 114
RST = 24
< STR = 180 - (114 + 24)
= 180 - 138
= 42\(^o\)
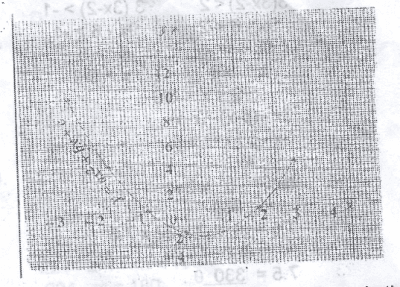
The graph of y = \(ax^2 + bx + c\) is shown oon the diagram. Find the minimum value of y
-2, 0
-2, 1
-2, 3
-2, 5
Correct answer is B
No explanation has been provided for this answer.
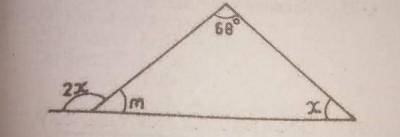
Find the value of m in the diagram
72\(^o\)
68\(^o\)
44\(^o\)
34\(^o\)
Correct answer is C
2x + m = 180
x + m = 112
x = 122 - m
2(112 - m) + m = 180
224 - 2m + m = 180
224 - m = 180
224 - 180 = m
m = 44\(^o\)
The diagonal of a square is 60 cm. Calculate its peremeter
20\(\sqrt{2}\)
40\(\sqrt{2}\)
90\(\sqrt{2}\)
120\(\sqrt{2}\)
Correct answer is D

\(60^2 + x^2 + x^2\)
\(360^2 = 2x^2\)
\(x^2\) = 1800
x = \(\sqrt{1800}\)
x = 42.4264
x = 42.4264
perimeter = 4x
= 4 x 42.4264
= 169.7056
= 120\(\sqrt{2}\)
= 120\(\sqrt{2}\)
36.87\(^o\)
39.70\(^o\)
51.34\(^o\)
53.13\(^o\)
Correct answer is C
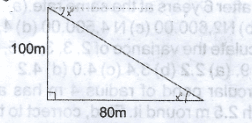
Tan \(x^o = \frac{100m}{80}\)
Tan \(x^o = Tan^{-1} 1.25\)
x = 51.34\(^o\)
WAEC Subjects
Aptitude Tests