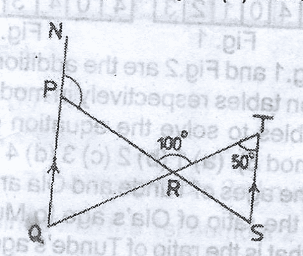
In the diagram, NQ//TS, <RTS = 50\(^o\) and <PRT = 100\(^o\). Find the value of <NPR
110\(^o\)
130\(^o\)
140\(^o\)
150\(^o\)
Correct answer is B
< TSR = 180 - (80 + 50)
= 180 - (130)
= 50\(^o\)
< QPR = < TSR corresponding < s
< NPR + QPR = < NPR
180\(^o\) - < QPR = < NPR
180\(^o\) - 50 = < NPR
< NPR = 130\(^o\)
\(\frac{2}{9}\)
\(\frac{4}{9}\)
\(\frac{5}{9}\)
\(\frac{7}{9}\)
Correct answer is B
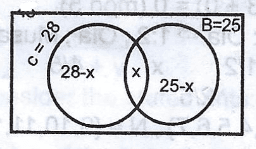
28 - x + x + 25 - x = 45
53 - x = 45
x = 53 - 45
x = 8
chemistry only = 28 - 8
= 20
Probability = \(\frac{20}{45}\)
= \(\frac{4}{9}\)
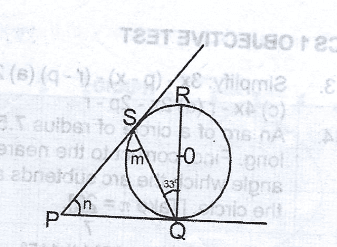
103\(^o\)
123\(^o\)
133\(^o\)q
143\(^o\)
Correct answer is B
< SQP = 180 - (90 + 33) < on a ----
= 180 - (123)
= 57\(^o\)
Therefore, (m + n) = 123\(^o\)
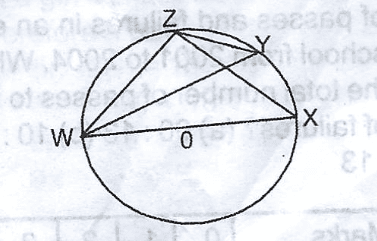
The diagram shows a circle O. If < ZYW = 33\(^o\) , find < ZWX
33\(^o\)
57\(^o\)
90\(^o\)
100\(^o\)
Correct answer is C
In ZY = 90\(^o\) < subtends In a semi O
ZWY = 180 - (90\(^o\) + 33)
= 57
ZWX = 57 + 33 = 90\(^o\)
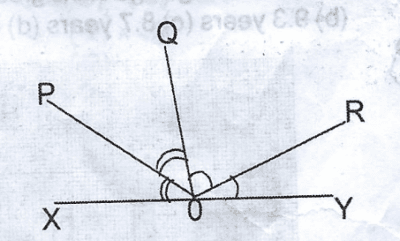
In the diagram, XY is a straight line.
60\(^o\)
90\(^o\)
100\(^o\)
120\(^o\)
Correct answer is B
<POX = <POQ; <ROY = QOR
2 <POQ + 2 <ROY = 180
2(<POQ = <ROY) = 180
<POQ + <ROY = 90
WAEC Subjects
Aptitude Tests