Solve the equation 2x - 3y = 22; 3x + 2y = 7
-5
-4
4
5
Correct answer is B
2x - 3y = 22 ---- eqn I
3x + 2y = 7 ---- eqn II
multiply eqn I by 2
4x - 6y = 44 ---- eqn III
multiply eqn II by 3
9x + 6y = 21 ---- eqn IV
Adding eqn III and IV
=> 13x = 65 => x = 5
Substituting 5 for x in eqn II
3x5 + 2y = 7 => 2y = -8
y = -4
What is the diameter of a circle of area 77cm2 [Take \(\pi = \frac{22}{7}\)]
\(\frac{\sqrt{2}}{7}cm\)
\(3\frac{1}{2}cm\)
7cm
\(7\sqrt{2}cm\)
Correct answer is D
\(A=\pi r^2 \Rightarrow 77 = \frac{22}{7} \times \frac{r^2}{1}\Rightarrow r^2 = \frac{77\times 7}{22} \Rightarrow r^2 = \frac{49}{2}\\
\Rightarrow r = \sqrt{\frac{49}{2}}=\frac{7}{\sqrt{2}}. Since D = 2r ∴ D = 2 \times \frac{7}{\sqrt{2}} = \frac{14}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = 7\sqrt{2}cm\)
026o
045o
210o
240o
Correct answer is D
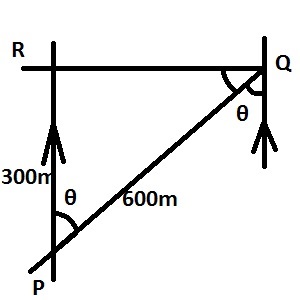
\(cos\theta = \frac{adj}{hyp}=\frac{300}{600}=\frac{1}{2}\\
\theta = cos^{-1}(0.5000)=60^{\circ}\)
The bearing of P from \(Q = \theta + 180 = 60 + 180 = 240^{\circ}\)
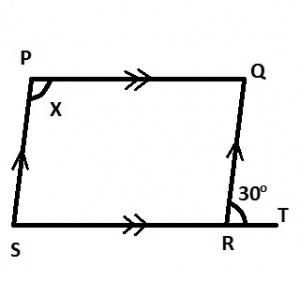
In the diagram, PQRS is a parallelogram and ∠QRT = 30o. Find x
95o
100o
120o
150o
Correct answer is D
Since ∠QRS = 180o - 30o = 150o and ∠SPQ = ∠QRS (theorem opp. angles in a parallelogram are equal) ∴ x = 150o
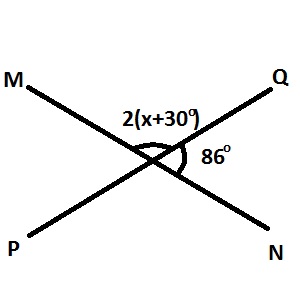
In the diagram PQ and MN are straight lines. Find the value of x
13o
17o
28o
30o
Correct answer is B
The straight line MN = 180 = 2(x+30o) + 86o =>
180 = 2x + 60o + 86o => 180o = 2x + 146o => 2x = 180 - 46 = 34o => x = 34/2 = 17o
WAEC Subjects
Aptitude Tests