Find the range of values of x for which\(\frac{x+2}{4}-\frac{x+1}{3}>\frac{1}{2}\)
x > 4
x > -4
x < 4
x < -4
Correct answer is D
\(\frac{x+2}{4}-\frac{x+1}{3}>\frac{1}{2}\\
\frac{3(x+2)-4(x+1)>6}{12}; 3x + 6 – 4x – 4 > 6\
-x +2>6; -x > 4; x < -4\)
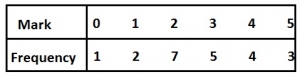
\(\frac{1}{11}\)
\(\frac{5}{22}\)
\(\frac{7}{22}\)
\(\frac{6}{11}\)
Correct answer is D
Prob (2 or 3) = prob(2) + prob(3)
Prob (mark 2) \(=\frac{7}{22}\) + Prob(mark 3) = \(\frac{5}{22}\)
Prob(2 or 3) \(=\frac{7}{22}+\frac{5}{22}=\frac{12}{22}=\frac{6}{11}\)

1
2
3
4
Correct answer is C
Median = 0, 1, 1, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5
Median mark = \(\frac{3+3}{2} = \frac{6}{2} = 3\)
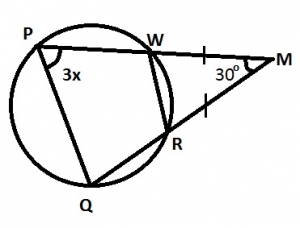
10o
25o
35o
60o
Correct answer is B
MPQ = PQM = 3x; ∆MPQ
MPQ + PQM + PMQ = 180° 3x + 3x + 30° = 180°
\(6x \times 30° = 180° 6x + 180° - 30°; 6x + 150°\)
\(x = \frac{150}{6} = 25^{\circ}\)
Given that \(\sqrt{128}+\sqrt{18}-\sqrt{K} = 7\sqrt{2}\), find K,
8
16
32
48
Correct answer is C
\(\sqrt{128} +\sqrt{18}-\sqrt{k}=7\sqrt{2}\\
\sqrt{2\times 64}+\sqrt{9\times 2} - \sqrt{k} = 7\sqrt{2}\\
8\sqrt{2} + 3\sqrt{2} - \sqrt{k} = 7\sqrt{2}; 11\sqrt{2} - \sqrt{k} = 7\sqrt{2}\\
-\sqrt{k}=7\sqrt{2}-11\sqrt{2}; -\sqrt{k} = -4\sqrt{2}; \sqrt{k}=4\sqrt{2}\\
=\sqrt{4^2\times 2} = \sqrt{16\times 2}; \sqrt{k}=\sqrt{32}; k = 32\)
WAEC Subjects
Aptitude Tests