Given that ξ = {1, 2, 3, . . . . . . ,10}, P= (x : x is prime) and Q = {y : y is odd}, find Pl∩Q
{2}
{1,9}
{315.7}
{4, 6, 8, 10}
Correct answer is B
ξ = {1, 2, 3, . . . . . . ,10}, P= (2, 3, 5, 7) and Q = {1, 3, 5, 9},
Pl∩Q = {1, 4, 6, 8, 9, 10}∩{1, 3, 5, 7, 9} = {1, 9}
Find the sum of the roots of the equation 2x2 + 3x - 9 = 0
-18
-6
\(-\frac{9}{2}\)
\(-\frac{3}{2}\)
Correct answer is D
The general quadratic equation
x2 - (sum of roots) x + (product of root) = 0
Comparing with the given equation
2x2 +3x2 - 9 = 0; \(x^2 + \frac{3}{2}x - \frac{9}{2} = 0\\
Sum \hspace{1mm} of \hspace{1mm}roots = -\frac{3}{2}\)
What is the volume of a solid cylinder of diameter 7cm and height 7cm? (Take \(\pi = \frac{22}{7}\))
38.5cm3
77cm3
269.5cm3
1078cm3
Correct answer is C
Volume of a solid cylinder = Base area x height
Base area \(=\pi r^2 =\frac{22}{7} \times \frac{7}{2}\times \frac{7}{2} = \frac{77}{2}\)
Volume of a solid cylinder = \(\frac{77}{2}\times \frac{7}{1} = \frac{539}{2}cm^3\\
=269.5cm^3\)
9(3px - 4y)2
3(3px - 4y)(3px - 4y)
9(px - 4y)(3p x + 4y)
3(3px -4y)(3px +4y)
Correct answer is D
27p2x2 - 48y2; 3(32 p2x2-42y2)
3[(3px) 2 - (4y) 2]; 3[(3px-4y)(3px+4y)]
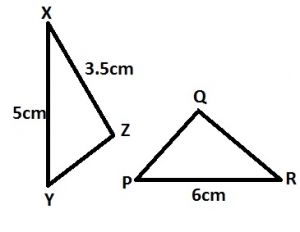
In the diagram, ∆XYZ is similar to ∆PRQ, |XY| = 5cm, |XZ| =3.5cm and |PR| = 8cm. Find |PQ|
5.6 cm
11.2cm
11.4cm
28.0cm
Correct answer is A
\(\frac{PQ}{PR}=\frac{XZ}{XY}; \frac{PQ}{8}=\frac{3.5}{5}\\
PQ=\frac{8\times 3.5}{5}=\frac{28}{5}=5.6cm\)
WAEC Subjects
Aptitude Tests