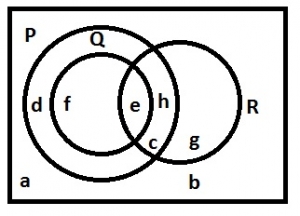
From the Venn Diagram below, find Q' ∩ R.
(e)
(c, h)
(c, g, h)
(c, e, g, h)
Correct answer is C
Q' ∩ R Q' = U - Q Q' = {a, b, c, d, g, h, i} R = {c, e, h, g} Q' ∩ R = {c, h, g}
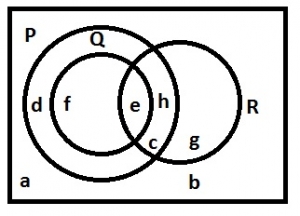
From the Venn diagram below, how many elements are in P∩Q?
1
2
4
6
Correct answer is B
P \(\cap\) Q = {f, e} = 2
If \(P = \sqrt{QR\left(1+\frac{3t}{R}\right)}\), make R the subject of the formula.
\(R = \frac{3Qt}{P^2 - Q}\)
\(R = \frac{P^2 – 3t}{Q+1}\)
\(R = \frac{P^2 + 3t}{Q - 1}\)
\(R = \frac{P^2-3Qt}{Q}\)
Correct answer is D
No explanation has been provided for this answer.
2√3
4√3
6√3
12√3
Correct answer is B
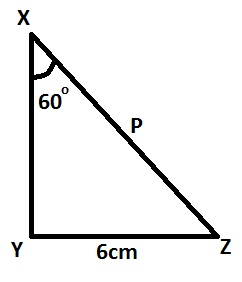
\(sin \theta = \frac{opp}{hyp}\\
sin 60^o = \frac{|YZ|}{|XZ|}=\frac{6}{P}\\
P sin 60^o = 6\\
P = \frac{6}{sin60^o}\\
=\frac{6}{\sqrt{\frac{3}{2}}}=4\sqrt{3}\)
I only
II only
III only
I and III only
Correct answer is B
Using the formula, \((n - 2) \times 180°\) to get the sum of the interior angles. Then we can have
\((n - 2) \times 180° = 108n\) ... (1)
\((n - 2) \times 180° = 116n\) ... (2)
\((n - 2) \times 180° = 120n\) ... (3)
Solving the above given equations, where n is not a positive integer then that angle is not the interior for a regular polygon.
(1): \(180n - 360 = 108n \implies 72n = 360\)
\(n = 5\) (regular pentagon)
(2): \(180n - 360 = 116n \implies 64n = 360\)
\(n = 5.625\)
(3): \(180n - 360 = 120n \implies 60n = 360\)
\(n = 6\) (regular hexagon)
Hence, 116° is not an angle of a regular polygon.
WAEC Subjects
Aptitude Tests