If \(\frac{3^{(1-n)}}{9^{-2n}}=\frac{1}{9}\) find n
\(-\frac{3}{2}\)
\(\frac{1}{3}\)
-1
-3
Correct answer is C
\(\frac{3^{(1-n)}}{9^{-2n}}=\frac{1}{9}\\
3^{1-n}\times 3^{-2(-2n)} = 3^{-2}\\
1-n-2(-2n)= -2\\
1-n+4n=-2\\
n=-1\)
0.01014
0.01021
0.01015
0.01016
Correct answer is A
option A CANNOT BE BECAUSE THE LAST NUMBER BEFORE 1 CAN ONLY BE ROUNDED DOWN TO ZERO.
Evaluate \((111_{two})^2 - (101_{two})^2\)
10two
100two
1100two
11000two
Correct answer is D
\((111_{2})^2 - (101_{2})^2\)
Difference of two squares
\((111 - 101)(111 + 101)\)
= \((10)(1100)\)
= \(11000_{2}\)
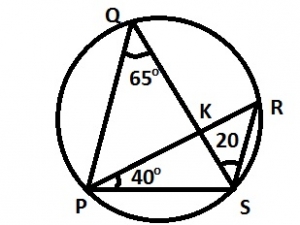
85o
60o
55o
45o
Correct answer is C
< QPS = < PRS = 65° (angles in the same segment)
< PSR + 40° + 65° = 180°
< PSR + 105° = 180°
< PSR = 75°
< PSR = < PSQ + < QSR
75° = < PSQ + 20° \(\implies\) < PSQ = 75° - 20° = 55°
Find the values of x for which \( \frac{1}{2x^2 - 13x +15} \) is not defined,
5 or \( \frac{3}{2} \)
1 or \( \frac{15}{13} \)
2 or 15
13 or 15
Correct answer is A
The fraction is undefined when the denominator is equal to zero
\(2x^2 - 13x + 15 = 0\\
2x^2 - 3x - 10x + 15\\
x(2x-3)-5(2x-3) = 0\\
(2x-3)(x-5)=0\\
x = \frac{3}{2} or x = 5\)
WAEC Subjects
Aptitude Tests