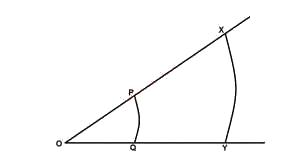
1:3
1:6
1:9
2:3
4:9
Correct answer is C
Let the radius of the arc PQ = r and the radius of the arc XY = R.
Length of arc PQ = \(\frac{\theta}{360} \times 2\pi r = 1\)
Length of arc XY = \(\frac{\theta}{360} \times 2\pi R = 3\)
Ratio of the arc = \(\frac{r}{R} = \frac{360 \times 2\pi \theta}{2\pi \theta \times 360 \times 3}\)
= \(\frac{1}{3}\)
Ratio of their area = \((\frac{1}{3})^2 = \frac{1}{9}\)
= 1 : 9
Find the area of an equivalent triangle of side 16cm
64√3cm2
72√3cm2
96cm2
128√3cm2
128cm2
Correct answer is A
Area = 1/2 x 16 x 16sin60o = 64√3cm2
4πεoq2r
qr/4πεo
q/4πεor
q2/4πεor
q2/4πεo
Correct answer is C
No explanation has been provided for this answer.
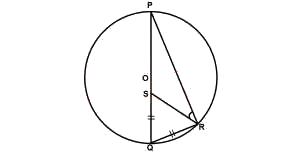
In the diagram above, O is the center of the circle, |SQ| = |QR| and ∠PQR = 68°. Calculate ∠PRS
34o
45o
56o
62o
68o
Correct answer is A
From the figure, < PQR = 68°
\(\therefore\) < QRS = < QSR = \(\frac{180 - 68}{2}\) (base angles of an isos. triangle)
= 56°
\(\therefore\) < PRS = 90° - 56° = 34° (angles in a semi-circle)
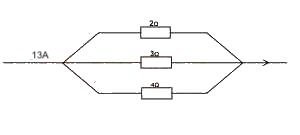
Calculate the current in the 3Ω resistor shown in
the diagram above.
3.0A
4.0A
4.3A
12.0A
39.0A
Correct answer is B
Total Resistance R = 1/R = 1/R1 + 1/R2 + 1/R3
R = 12/13Ω
V = IR = (12/13) x 13 = 12v
1 across 3Ω = V/R = 12/3 = 4A
WAEC Subjects
Aptitude Tests