40
5
6
8
12
Correct answer is D
Let x be the exterior angle; interior = 3x; but x + 3x = 180o
4x = 180o; x = 45
= \(\frac{360}{45}\) = 8
7 x10-20N
7 x 10-5N
7 x10-2N
7 x103N
7x100N
Correct answer is C
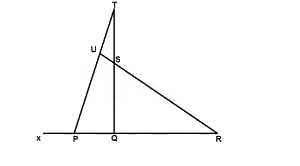
In the diagram above, ∠PTQ = ∠URP = 25° and XPU = 4URP. Calculate ∠USQ.
100o
120o
125o
130o
150o
Correct answer is D
Since < URP = 25°, then < XPU = 4 x 25° = 100°
\(\therefore\) < TPQ = 180° - 100° = 80°
\(\therefore\) < PQT = 180° - (80° + 25°) = 75°
< SQR = 75° - 25° = 50° (exterior angle = 2 opp interior angles)
\(\therefore\) < USQ = 180° - 50° = 130°
Yellow and red
Orange and green
Violet and blue
Blue and green
Red and indigo
Correct answer is E
No explanation has been provided for this answer.
The angles of a pentagon are x°, 2x°, (x + 60)°, (x + 10)°, (x -10)°. Find the value of x.
40
60
75
80
90
Correct answer is D
Sum of ∠s in a pentagon = (n - 2)180 = 540°
x° + 2x° + x° + 60° + x° + 10° + x° - 10° = 540°
6x° + 60° = 540°; x = 80°
WAEC Subjects
Aptitude Tests